
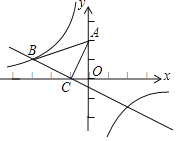
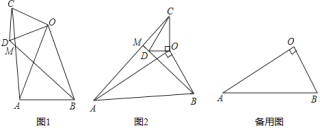
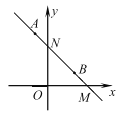
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ�б�������������ϣ���C����Ϊ����1��0����tan��ACO��2��һ�κ���y��kx+b��ͼ����B��C������������y��![]() ��ͼ����B��
��ͼ����B��
��1����һ�κ�����ϵʽ�ͷ����������Ĺ�ϵʽ��
��2����x��0ʱ��kx+b��![]() ��0�Ľ⼯Ϊ�� ����
��0�Ľ⼯Ϊ�� ����
��3����x����������E��F����E�ڵ�F����ߣ���EF��1�����ı���ABEF�ܳ���Сʱ����ֱ��д����E�ĺ�����Ϊ�� ����
���𰸡���1��y����![]() x��
x��![]() ��y����
��y����![]() ����2����3��x��0����3��-
����2����3��x��0����3��-![]()
��������
��1������B��BF��x���ڵ�F���ɡ�AOC�ա�CFB��õ�B�����꣬���ô���ϵ���������һ�κ����ͷ����������Ĺ�ϵʽ��
��2����x��0ʱ�����һ�κ���ֵy��kx��bС�ڷ���������y��![]() ��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��3����B����ƽ��1����λ�õ�B�䣨2��1��������A����x��ĶԳƵ�A�䣨0��2��������A��B�佻x���ڵ�F�����ֱ��A��B��Ľ���ʽ�����F�����꼴�ɽ�����⣮
�⣺��1����ͼ1�У�����B��BF��x���ڵ�F��

����C��������1��0����
��OC��1��
��tan��ACO��2��![]() ��
��
��OA��2��
���A������0��2����
��OA��2��OC��1��
�ߡ�BCA��90����
���BCF+��ACO��90����
���ߡ�CAO+��ACO��90����
���BCF����CAO��
���AOC�ա�CFB��AAS����
��FC��OA��2��BF��OC��1��
����B����������3��1����
����B��������뷴������������ʽ�ɵã�1��![]() ����ã�m����3��
����ã�m����3��
�ʿɵ÷�������������ʽΪy����![]() ��
��
����B��C���������һ�κ�������ʽ�ɵã�
![]() ����ã�
����ã�  ��
��
�ʿɵ�һ�κ�������ʽΪy����![]() x��
x��![]() ��
��
��2����ϵ�B�����꼰ͼ�ɵõ�x��0ʱ��kx+b��![]() ��0�Ľ⼯Ϊ����3��x��0��
��0�Ľ⼯Ϊ����3��x��0��
�ʴ�Ϊ����3��x��0��
��3����ͼ�У���span>B����ƽ��1����λ�õ�B�䣨2��1��������A����x��ĶԳƵ�A�䣨0��2��������A��B�佻x���ڵ�F��
��ֱ��A��B��Ľ���ʽΪax+b��a��0��
��A�䣨0��2����B�䣨2��1�������![]()
���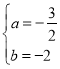
��ֱ��A��B��Ľ���ʽΪy��![]() x2��
x2��
����y=0����![]() x2=0
x2=0
���x=-![]()
��F��![]() ��0����
��0����
��OF��![]()
��OE��1��![]() ��
��![]()
���E�ĺ�����Ϊ![]() ��
��
�ʴ�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��:��ͼ��1��������OAB����OCD�У�OA��OB��OC��OD����AOB����COD��36��������AC��BD���ڵ�M����![]() ��ֵΪ�� �����ڡ�AMB�Ķ���Ϊ�� ����
��ֵΪ�� �����ڡ�AMB�Ķ���Ϊ�� ����
��2�����̽�� :��ͼ��2��������OAB����OCD�У���AOB����COD��90������OAB����OCD��30��������AC����BD���ӳ����ڵ�M�������![]() ��ֵ����AMB�Ķ�����
��ֵ����AMB�Ķ�����
��3����չ����:�ڣ�2���������£�����OCD�Ƶ�O��ƽ������ת��AC��BD����ֱ�߽��ڵ�M����OD��1��OB��![]() ����ֱ��д������C���M�غ�ʱAC�ij���
����ֱ��д������C���M�غ�ʱAC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ��������Ӧ�����⣮
��������
���ճ������У���֧����ȡ������ȶ���Ҫ���룮��һ������ʽ�ֽ���������ij�������䣮���磺���ڶ���ʽ![]() ����ʽ�ֽ�Ľ����
����ʽ�ֽ�Ľ����![]() ����ȡ
����ȡ![]() ��
��![]() ���������ʽ��ֵ�ֱ���
���������ʽ��ֵ�ֱ���![]() ��
��![]() ��
��![]() �����ǾͿ�����
�����ǾͿ�����![]() ����Ϊһ����λ��������
����Ϊһ����λ��������
��������
��1���������е�ԭ������ȡ![]() ��
��![]() �����ɵ�������_______��
�����ɵ�������_______��
��2������������Ϊ����ʽ![]() ��ʽ�ֽ�Ľ����ȡ
��ʽ�ֽ�Ľ����ȡ![]() ��
��![]() ʱ����Դ
ʱ����Դ![]() ��
��![]() �³����������������������������Ƕ��٣���д��һ�ּ��ɣ�
�³����������������������������Ƕ��٣���д��һ�ּ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ļӿ��Լ������ֻ����ռ������������ΪԽ��Խ���û��IJ�������ϰ�ߣ��ɴ˴�����һ���������ƽ̨����֪ij����ƽ̨���Ͳͷ������Ͳ;����йأ���ƽֻ̨��5ǧ��Χ�����ͣ���Ϊ�����Ͳ�Ա���Ͳ����룬�ִӸ�ƽ̨�����ȡ80�����������û�����ͳ�ƣ����Ͳ;������ͳ�ƽ�����±���
�Ͳ;���x��ǧ�ף� | 0 | 1 | 2 | 3 | 4 |
���� | 12 | 20 | 24 | 16 | 8 |
��1������80�����������û�����ȡһ���û������û����Ͳ;��벻����3ǧ�ĸ���Ϊ ��
��2������80���û��Ͳ;���Ϊ������ͬһ������ȡ��С�����ݵ��м�ֵ������ڶ�С�飨1��x ��2�����м�ֵ��1.5�����Թ������ø�ƽ̨�������û���ƽ���Ͳ;��룻
��3����������ƽ̨���Ͳ�Ա���Ͳͷ������Ͳ;����йأ�������2ǧ��ʱ��ÿ��3Ԫ������2ǧ������4ǧ��ʱ��ÿ��5Ԫ������4ǧ��ʱ��ÿ��9Ԫ�� �Ը���80���û������Ͳͷ��õ�ƽ����Ϊ���ݣ����Ͳ�Աһ���Ŀ�����벻����150Ԫ���Թ���һ������Ҫ�Ͷ��ٷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
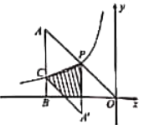
����Ŀ����ͼ��PΪ˫����![]() ��һ����.����OP���ӳ�����A��ʹ
��һ����.����OP���ӳ�����A��ʹ![]() ������A��x��Ĵ��ߣ�����ΪB����˫�����ڵ�C.��
������A��x��Ĵ��ߣ�����ΪB����˫�����ڵ�C.��![]() ʱ������PC����
ʱ������PC����![]() ��ֱ��PC���з��ۣ����ۺ��
��ֱ��PC���з��ۣ����ۺ��![]() ���ı���BOPC���ص����֣�ͼ����Ӱ���֣��������_______________
���ı���BOPC���ص����֣�ͼ����Ӱ���֣��������_______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c�ĶԳ�����x��![]() ��С��ͨ���۲�ó�������������Ϣ����
��С��ͨ���۲�ó�������������Ϣ����![]() ����abc<0����4a+2b+c>0����2a+3b=0������Ϊ������ȷ����_________________��
����abc<0����4a+2b+c>0����2a+3b=0������Ϊ������ȷ����_________________��
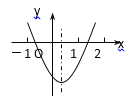
A.�٢�B.�ڢ�C.�٢�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���
���![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����������
����������![]() ��ֱ��
��ֱ��![]() ��������ͬ�Ľ��㣬����һ���������߶�
��������ͬ�Ľ��㣬����һ���������߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() �����˵㣩����һ���������߶�
�����˵㣩����һ���������߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() �����˵㣩����
�����˵㣩����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
A. ![]() B.
B. ![]() ��
��![]() C.
C. ![]() D.
D. ![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
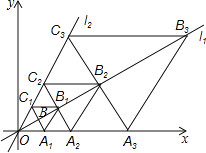
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() ��ֱ��
��ֱ��![]() ����ֱ��
����ֱ��![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ���Ե�
���Ե�![]() Ϊ�Գ����ģ�����
Ϊ�Գ����ģ�����![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ���õ��ı���
���õ��ı���![]() �����Ե�
�����Ե�![]() Ϊ�Գ����ģ���
Ϊ�Գ����ģ���![]() ��ĶԳƵ�
��ĶԳƵ�![]() ������
������![]() ��
�� ![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ���õ��ı���
���õ��ı���![]() ���������˹�������ȥ�����ı���
���������˹�������ȥ�����ı���![]() �������___________��
�������___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ���ڡ�Σ�շ����������������Ⱦ������ij��ҩ�ಿ��Ϊ���˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������飮
��1������ѡȡ�����ķ����������һ����____________����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ��
����ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ��
����ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
���������鷢�֣����ܵ���ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��
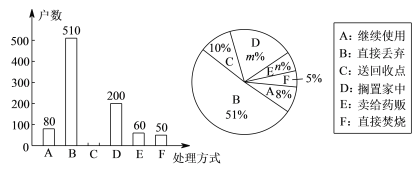
��2����գ�m=______��n=_____��
��3����ȫ����ͳ��ͼ��
��4�����������ͥ��������ҩƷ����ķ�ʽ�� ����ֻ����ţ�
��5����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com