
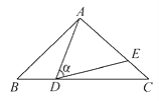
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是________.(把你认为正确结论的序号都填上)
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是________.(把你认为正确结论的序号都填上)
【答案】①②④
【解析】
作AH⊥BC于H,如图,根据等腰三角形的性质易得∠B=∠ADE=∠C,于是可判断△ADE∽△ACD;在Rt△ABH中,利用三角函数的定义可计算出BH=8,则BC=2BH=16,所以当BD=6,则CD=10=AB,再证明∠EDC=∠BAD,则可判断△ABD≌△DCE;先证明△ABD∽△DCE,分类讨论:当∠DEC=90°,则∠ADB=90°,可得BD为8;当∠EDC=90°,则∠BAD=90°,根据三角函数定义可得BD=![]() ;设BD=x,则CD=16-x,由△ABD∽△DCE,利用相似比可得CE=-
;设BD=x,则CD=16-x,由△ABD∽△DCE,利用相似比可得CE=-![]() ,然后根据二次函数的性质可得CE的最大值为6.4,于是有0<CE≤6.4.
,然后根据二次函数的性质可得CE的最大值为6.4,于是有0<CE≤6.4.
解:作AH⊥BC于H,如图,
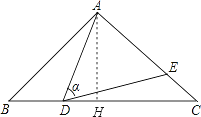
∵AB=AC,
∴∠B=∠C=α,BH=CH,
而∠ADE=∠B=α,
∴∠ADE=∠C,
而∠DAE=∠CAD,
∴△ADE∽△ACD,所以①正确;
在Rt△ABH中,cosB=![]() ,
,
∴BH=10×![]() =8,
=8,
∴BC=2BH=16,
当BD=6,则CD=10,
∵∠ADC=∠B+∠BAD,
而∠ADE=∠B=α,
∴∠EDC=∠BAD,
在△ABD与△DCE中
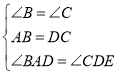 ,
,
∴△ABD≌△DCE,所以②正确;
∵∠B=∠C,∠BAD=∠CDE,
∴△ABD∽△DCE,
△DCE为直角三角形,当∠DEC=90°,则∠ADB=90°,BD为8;
当∠EDC=90°,则∠BAD=90°,BD=![]() ,所以③错误;
,所以③错误;
设BD=x,则CD=16-x,
由△ABD∽△DCE得![]() ,即
,即![]() ,
,
∴CE=-![]() ,
,
∴CE的最大值为6.4,
∴0<CE≤6.4,所以④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
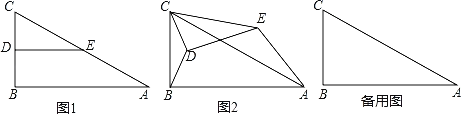
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发市场内有一种水果,保鲜期一周,如果冷藏,可以延长保鲜时间,但每天仍有一定数量的这种水果变质,假设这种水果保鲜期内的个体重量基本保持不变。现有一个体户,按市场价收购了这种水果200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后这种鲜水果每千克的价格每天可上涨0.2元,但存放一天需各种费用20元,日平均每天还有1千克变质丢弃.
(1)设![]() 天后每千克鲜水果的市场价
天后每千克鲜水果的市场价![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若存放![]() 天后将鲜水果一次性出售,设鲜水果的销售总金额为
天后将鲜水果一次性出售,设鲜水果的销售总金额为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)该个体户将这批水果存放多少天后出售,可获最大利润![]() ?最大利润
?最大利润![]() 是多少?
是多少?
(本题不要求写出自变量![]() 的取值范围)
的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
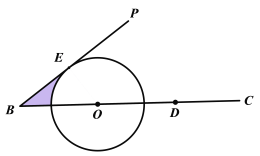
【题目】如图,已知∠PBC,在射线BC上任取一点D,以线段BD的中点O为圆心作⊙O,且⊙O与PB相切于点E.
(1)求作:射线BP上一点A,使△ABD为等腰三角形,且AB=AD.(要求:运用直尺和圆规,保留作图痕迹,不写作法)
(2)求证:AD是⊙O的切线.
(3)若BD的长为8cm,∠PBC=30°,求阴影部分的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距![]() 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是
一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是![]() 以快车开始行驶计时,设时间为
以快车开始行驶计时,设时间为![]() , 两车之间的距离为
, 两车之间的距离为![]() ,图中的折线是
,图中的折线是![]() 与
与![]() 的函数关系的部分图象,根据图象解决以下问题:
的函数关系的部分图象,根据图象解决以下问题:

(1)慢车的速度是_ _![]() ,点
,点![]() 的坐标是_ _;
的坐标是_ _;
(2)线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式是_ ;
之间的函数关系式是_ ;
(3)试在图中补全点![]() 以后的图象.
以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )

A.∠A=60°B.△ACD是直角三角形
C.BC=![]() CDD.点B是△ACD的外心
CDD.点B是△ACD的外心
查看答案和解析>>
科目:初中数学 来源: 题型:
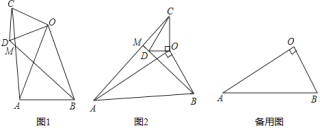
【题目】(1)问题发现:如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=36°,连接AC,BD交于点M.①![]() 的值为 ;②∠AMB的度数为 ;
的值为 ;②∠AMB的度数为 ;
(2)类比探究 :如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数.
的值及∠AMB的度数.
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com