
【题目】商场销售一批衬衫,每天可售出20件,每件盈利40元,为了扩大销售,减少库存,决定采取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.
(1)若商场每天要盈利1200元,每件应降价多少元?
(2)设每件降价x元,每天盈利y元,每件降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
【答案】(1)20元 (2)15元;1250元
【解析】
(1) 设每件降价x元,盈利为y,则销售了(20+2x)件,得到![]() ,令y=1200,得到
,令y=1200,得到![]() ,整理得
,整理得![]() ,然后利用因式分解法解求解即可得到答案;
,然后利用因式分解法解求解即可得到答案;
(2) 把y=-2x2+60x+800配成顶点式得到y=-2(x-15)2+1250,然后根据二次函数的最值问题即可得到答案.
解:(1)设每件降价x元,盈利为y,则销售了(20+2x)件,
![]()
令y=1200,
∴![]() ,
,
整理得![]() ,
,
即:![]()
解得x1=10(因要减少库存,舍去),x2=20,
所以商场每天要盈利1200元,每件衬衫降价20元;
答:降价20元时可降低库存,并使每天盈利1200元;
(2)根据题意得到:![]()
即:![]()
当x=15元时,有最大值y=1250,
每件降价15元时商场每天的盈利达到最大1250元.


科目:初中数学 来源: 题型:
【题目】(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
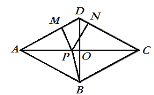
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为_____.
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
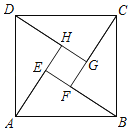
【题目】某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形,设小正方形的边长m,直角三角形较短边长n,且n=2m﹣4,大正方形的面积为S.
(1)求S关于m的函数关系式.
(2)若小正方形边长不大于3,当大正方形面积最大时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,E为AB边上一点,将△BEC沿CE翻折,点B落在点F处,当△AEF为直角三角形时,BE=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
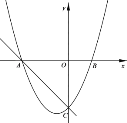
【题目】已知在平面直角坐标系中,抛物线![]() 与x轴相交于点A,B,与y轴相交于点C,直线y=-x-4经过A,C两点,
与x轴相交于点A,B,与y轴相交于点C,直线y=-x-4经过A,C两点,
(1)求抛物线的表达式;
(2)如果点P,Q在抛物线上(P点在对称轴左边),且PQ∥AO,PQ=![]() AO,求P,Q的坐标;
AO,求P,Q的坐标;
(3)动点M在直线y=-x-4上,且以C,O,M为顶点的三角形与△ABC相似,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
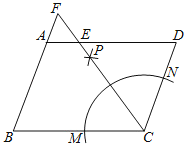
【题目】如图,ABCD中,CD=4,BC=6,按以下步骤作图:①以点C为圆心,适当长度为半径作弧,分别交BC,CD于M,N两点:②分别以点M,N为圆心,以大于![]() MN的长为半径画弧,两弧在ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( )
MN的长为半径画弧,两弧在ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( )
A.1B.2C.2.5D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com