
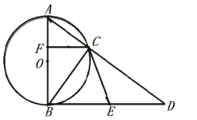
【题目】如图,⊙O是![]() ABC的外接圆,AB是圆的直径,直线AC与过B点的切线相交于点D,E是BD的中点,连接CE.
ABC的外接圆,AB是圆的直径,直线AC与过B点的切线相交于点D,E是BD的中点,连接CE.
(1)求证:CE是圆O的切线;
(2)如图,CF⊥AB,垂足为F,若⊙O的半径为3,BE=4,求CF的长.
【答案】(1)见解析 (2)![]()
【解析】
(1)根据圆周角定理由AB为⊙的直径得∠ACB=90°,根据直角三角形斜边上的中线性质结合等边对等角,所以有∠1+∠2=∠3+∠4,证得OC⊥CE,然后根据切线的判定定理得CE是⊙O的切线;
(2)在Rt△ABD中,根据勾股定理计算出AD,再证明Rt△ABC∽Rt△ADB,利用相似比计算出AC,然后证明△ACF∽△ADB,利用相似比可计算得出结论.
(1)连接OC,
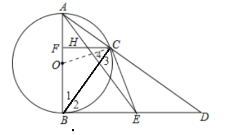
∵AB为⊙O的直径,且BD是⊙O的切线,
∴∠ACB=∠BCD=∠ABD=90°,
∵CE为斜边BD上的中线,
∴CE=BE=DE,
∴∠2=∠3,
∵OB=OC,
∴∠1=∠4
∴∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)∵BE=4,半径为3,
∴BD=2BE=8,AB=6,
在Rt△ABD中,
∴![]() ,
,
∵∠ACB=∠ABD=90°,
∴Rt△ABC∽Rt△ADB,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵CF⊥AB,
∴∠AFC=∠ABD=90°,
∴CF∥BD ,
∴△ACF∽△ADB,
∴![]() ,即
,即 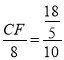
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图像经过点M(
的图像经过点M(![]() ,n),点N(
,n),点N(![]() ,n),交y轴于点A.
,n),交y轴于点A.
(1)求a,b满足的关系式;
(2)若抛物线上始终存在不重合的P,Q两点(P在Q的左边)关于原点对称.
①求a的取值范围;
②若点A,P,Q三点到直线l:![]() 的距离相等,求线段PQ长.
的距离相等,求线段PQ长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
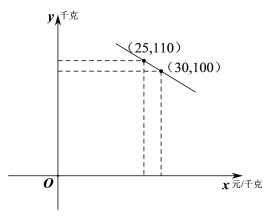
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
(Ⅰ)求证:AC是⊙O的切线;
(Ⅱ)若BF=5,DF=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A和∠B的平分线交于点P,过点P作PE⊥AB交AB于点E.若BC=5,AC=12,则AE等于______ .
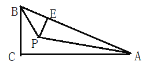
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
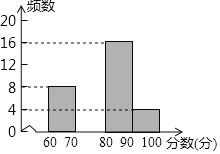
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC=![]() ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
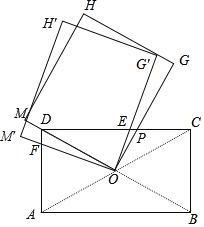
A.y=![]() xB.y=
xB.y=![]() xC.y=
xC.y=![]() xD.y=
xD.y=![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.
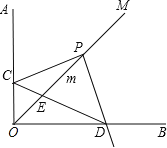
(1)如图,当点C、D都不与点O重合时,求证:PC=PD;
(2)联结CD,交OM于E,设CD=x,PE=y,求y与x之间的函数关系式;
(3)如图,若三角板的一条直角边与射线OB交于点D,另一直角边与直线OA,直线OB分别交于点C,F,且△PDF与△OCD相似,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
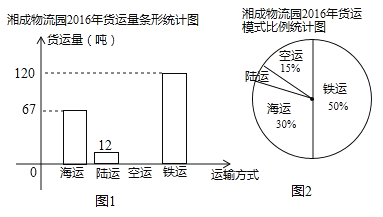
【题目】在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com