
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线经过点D(﹣2,﹣3)和点E(3,2),点P是第一象限抛物线上的一个动点.
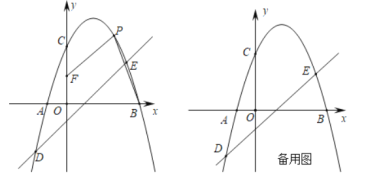
(1)求直线DE和抛物线的表达式;
(2)在y轴上取点F(0,1),连接PF,PB,当四边形OBPF的面积是7时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴的右侧时,直线DE上存在两点M,N(点M在点N的上方),且MN=2![]() ,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
【答案】(1)y=x﹣1,y=![]() x2+
x2+![]() x+2;(2)P(2,3)或(
x+2;(2)P(2,3)或(![]() ,
,![]() );(3)N(
);(3)N(![]() ,
,![]() ).
).
【解析】
(1)将点D、E的坐标代入函数表达式,即可求解;
(2)S四边形OBPF=S△OBF+S△PFB=![]() ×4×1+
×4×1+![]() ×PH×BO,即可求解;
×PH×BO,即可求解;
(3)过点M作A′M∥AN,过作点A′直线DE的对称点A″,连接PA″交直线DE于点M,此时,点Q运动的路径最短,即可求解.
(1)将点D、E的坐标代入函数表达式得:![]() ,解得:
,解得:
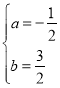 ,故抛物线的表达式为:y=
,故抛物线的表达式为:y=![]() x2+
x2+![]() x+2,
x+2,
同理可得直线DE的表达式为:y=x﹣1…①;
(2)如图1,连接BF,过点P作PH∥y轴交BF于点H,
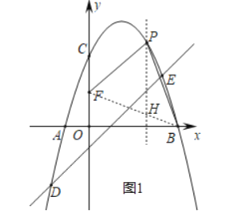
将点FB代入一次函数表达式,
同理可得直线BF的表达式为:y=![]() +1,
+1,
设点P(x,![]() ),则点H(x,
),则点H(x,![]() +1),
+1),
S四边形OBPF=S△OBF+S△PFB=![]() ×4×1+
×4×1+![]() ×PH×BO=2+2(
×PH×BO=2+2(![]() )=7,
)=7,
解得:x=2或![]() ,
,
故点P(2,3)或(![]() ,
,![]() );
);
(3)当点P在抛物线对称轴的右侧时,点P(2,3),
过点M作A′M∥AN,过作点A′直线DE的对称点A″,连接PA″交直线DE于点M,此时,点Q运动的路径最短,
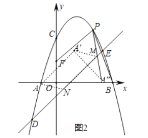
∵MN=2![]() ,相当于向上、向右分别平移2个单位,故点A′(1,2),
,相当于向上、向右分别平移2个单位,故点A′(1,2),
A′A″⊥DE,则直线A′A″过点A′,则其表达式为:y=﹣x+3…②,
联立①②得x=2,则A′A″中点坐标为(2,1),
由中点坐标公式得:点A″(3,0),
同理可得:直线AP″的表达式为:y=﹣3x+9…③,
联立①③并解得:x=![]() ,即点M(
,即点M(![]() ,
,![]() ),
),
点M沿BD向下平移2![]() 个单位得:N(
个单位得:N(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
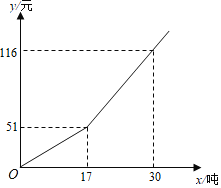
【题目】某市为了倡导居民节约用水,生活用自来水按阶梯式水价计费.如图是居民每户每月的水(自来水)费y(元)与所用的水(自来水)量x(吨)之间的函数图象.根据如图图象提供的信息,解答下列问题:
(1)当一户居民在某月用水为15吨时,求这户居民这个月的水费.
(2)当17≤x≤30时,求y与x之间的函数关系式;并计算某户居民上月水费为91元时,这户居民上月用水量多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB//CD,直线EF交AB于点E,交CD于点F,EP平分∠AEF,FP平分∠CFE,∠BEP=α,∠DFP=β,则a+β=( )
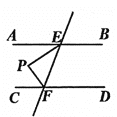
A.180°B.225°C.270°D.315°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的对称轴是y轴,且点(2,2),(1,![]() )在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
)在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
(1)求抛物线的解析式及顶点N的坐标;
(2)求证:四边形PMDA是平行四边形;
(3)求证:△DPE∽△PAM,并求出当它们的相似比为![]() 时的点P的坐标.
时的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
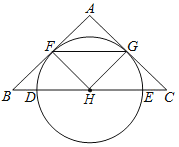
【题目】如图,在△ABC中,AB=AC,BC是经过⊙H的圆心,交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.
(1)求证:BH=CH;
(2)填空:①当∠FHG= 时,四边形FHCG是平行四边形;
②当∠FED= 时,四边形AFHG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垦利区在进行“五城同创”的过程中,决定购买A,B两种树对某路段进行绿化改造,若购买A种树1棵,B种树3棵,需要2250元;购买A种树2棵,B种树5棵,需要3900元.
(1)求购买A,B两种树每棵各需多少元?
(2)考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于52500元.若购进这两种树共100棵.问有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com