
【题目】如图,已知抛物线的对称轴是y轴,且点(2,2),(1,![]() )在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
)在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
(1)求抛物线的解析式及顶点N的坐标;
(2)求证:四边形PMDA是平行四边形;
(3)求证:△DPE∽△PAM,并求出当它们的相似比为![]() 时的点P的坐标.
时的点P的坐标.

【答案】(1)![]() , N(0,1);(2)证明见解析;(3)证明见解析,P(
, N(0,1);(2)证明见解析;(3)证明见解析,P(![]() ,4)或(﹣
,4)或(﹣![]() ,4).
,4).
【解析】
试题分析:(1)由已知点的坐标,利用待定系数法可求得抛物线的解析式,可求得其顶点N的坐标;
(2)设P点横坐标为t,则可表示出C、D、M、A的坐标,从而可表示出PA和DM的长,由PA=DM可证得结论;
(3)设P点横坐标为t,在Rt△PCM中,可表示出PM,可求得PM=PA,可知四边形PMDA为菱形,由菱形的性质和抛物线的对称性可得∠PDE=∠APM,可证得结论,在Rt△AOM中,用t表示出AM的长,再表示出PE的长,由相似比为![]() 可得到关于t的方程,可求得t的值,可求得P点坐标.
可得到关于t的方程,可求得t的值,可求得P点坐标.
试题解析:(1)解:∵抛物线的对称轴是y轴,∴可设抛物线解析式为![]() ,∵点(2,2),(1,
,∵点(2,2),(1,![]() )在抛物线上,∴
)在抛物线上,∴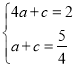 ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∴N点坐标为(0,1);
,∴N点坐标为(0,1);
(2)证明:设P(t,![]() ),则C(0,
),则C(0,![]() ),PA=
),PA=![]() ,∵M是O关于抛物线顶点N的对称点,D是C点关于N的对称点,且N(0,1),∴M(0,2),∵OC=
,∵M是O关于抛物线顶点N的对称点,D是C点关于N的对称点,且N(0,1),∴M(0,2),∵OC=![]() ,ON=1,∴DM=CN=
,ON=1,∴DM=CN=![]() ﹣1=
﹣1=![]() ,∴OD=
,∴OD=![]() ,∴D(0,
,∴D(0,![]() ),∴DM=2﹣(
),∴DM=2﹣(![]() )=
)=![]() =PA,且PM∥DM,∴四边形PMDA为平行四边形;
=PA,且PM∥DM,∴四边形PMDA为平行四边形;
(3)解:同(2)设P(t,![]() ),则C(0,
),则C(0,![]() ),PA=
),PA=![]() ,PC=|t|,∵M(0,2),∴CM=
,PC=|t|,∵M(0,2),∴CM=![]() ﹣2=
﹣2=![]() ,在Rt△PMC中,由勾股定理可得PM=
,在Rt△PMC中,由勾股定理可得PM=![]() =
=![]() =
=![]() =
=![]() =PA,且四边形PMDA为平行四边形,∴四边形PMDA为菱形,∴∠APM=∠ADM=2∠PDM,∵PE⊥y轴,且抛物线对称轴为y轴,∴DP=DE,且∠PDE=2∠PDM,∴∠PDE=∠APM,且
=PA,且四边形PMDA为平行四边形,∴四边形PMDA为菱形,∴∠APM=∠ADM=2∠PDM,∵PE⊥y轴,且抛物线对称轴为y轴,∴DP=DE,且∠PDE=2∠PDM,∴∠PDE=∠APM,且![]() ,∴△DPE∽△PAM;∵OA=|t|,OM=2,∴AM=
,∴△DPE∽△PAM;∵OA=|t|,OM=2,∴AM=![]() ,且PE=2PC=2|t|,当相似比为
,且PE=2PC=2|t|,当相似比为![]() 时,则
时,则![]() =
=![]() ,即
,即![]() =
=![]() ,解得t=
,解得t=![]() 或t=﹣
或t=﹣![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,4)或(﹣
,4)或(﹣![]() ,4).
,4).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒 ![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为 .
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式2x2+bx+c分解因式为2(x﹣3)(x+1),则b、c的值为( )
A.b=3,c=﹣1
B.b=﹣6,c=2
C.b=﹣6,c=﹣4
D.b=﹣4,c=﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com