
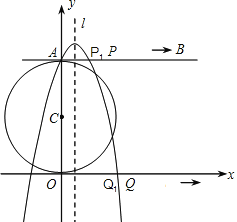
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
【答案】(1)y=![]() , l:x=
, l:x=![]() ;(2)t=2时,PQ与⊙C相切,P(2,8),Q(8,0);(3)N(1,7),理由见解析.
;(2)t=2时,PQ与⊙C相切,P(2,8),Q(8,0);(3)N(1,7),理由见解析.
【解析】
(1)先求出t=1时P1,Q1的坐标,然后用待定系数法即可得出抛物线的解析式,进而可求出对称轴l的解析式;
(2)当直线PQ与圆C相切时,连接CP,CQ,根据平行线的性质、角平分线的性质和三角形的内角和可得∠PCQ=90°,则有Rt△CMP∽Rt△QMC(M为PQ与圆C的切点),然后根据相似三角形的性质即可求出t的值;
(3)本题是典型的“将军饮马”问题,解题的关键是确定N的位置,可先利用待定系数法求出此时抛物线的解析式,然后作出P点关于直线l的对称点P′的坐标,连接P′Q,那么P′Q与直线l的交点即为所求的N点,至此只要求出直线P′Q的解析式,即可求出N点的坐标,问题即得解决.
解:(1)当t=1时,AP1=1,OQ1=4,则A、P1、Q1的坐标分别为A(0,8)、P1(1,8)、Q1(4,0),
设所求抛物线解析式为y=ax2+bx+c,则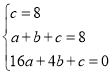 ,解得:
,解得: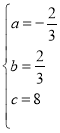
∴抛物线的解析式为y=![]() ,对称轴为直线l:x=
,对称轴为直线l:x=![]() ;
;
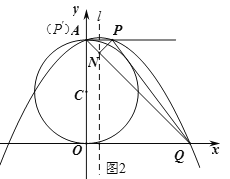
(2)设PQ与⊙C相切于点M,如图1,连接CP、CM、CQ,则PA=PM=t,QO=QM=4t,
∵CP、CQ分别平分∠APQ和∠OQP,∴![]() ,
,![]() ,
,
∵∠APQ+∠OQP=180°,∴∠CPQ+∠CQP=90°,
∴∠PCQ=![]() =90°,
=90°,
∵CM⊥PQ,∴可得Rt△CMP∽Rt△QMC,
∴![]() ,即
,即![]() ,∴t=±2,
,∴t=±2,
由于时间t只能取正数,所以t=2,即当运动时间t=2秒时,PQ与⊙C相切.
此时:P(2,8),Q(8,0);

(3)∵A(0,8),P(2,8),Q(8,0),∴设此时抛物线的解析式为![]() ,
,
把A,P,Q代入,得: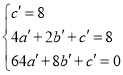 ,解得:
,解得: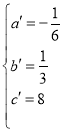 ,
,
∴抛物线的解析式为:y=![]() ,此时抛物线的对称轴为直线l:x=1,
,此时抛物线的对称轴为直线l:x=1,
作点P关于直线l的对称点P',如图2,则P'(0,8),即为点A,设P'Q与直线x=1交于点N,则此时NP+NQ最小,
∵P'(0,8),Q(8,0),∴直线P'Q的解析式为:y=﹣x+8,当x=1时,y=﹣1+8=7.
因此N点的坐标为(1,7).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为
,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为![]() ,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
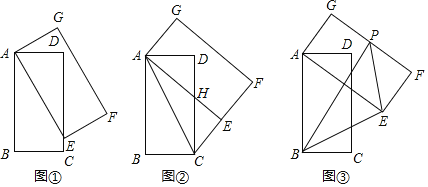
![]() 如图
如图![]() ,当点E落在DC边上时,直写出线段EC的长度为______;
,当点E落在DC边上时,直写出线段EC的长度为______;
![]() 如图
如图![]() ,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 直接写出线段DH的长度为______.
直接写出线段DH的长度为______.
![]() 如图
如图![]() 设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,
设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=4cm,P、Q两点同时从点C出发,点P沿从![]() 的方向运动,速度为2cm/秒;点Q沿从
的方向运动,速度为2cm/秒;点Q沿从![]() 的方向运动,速度为1cm/秒.当运动时间为t秒﹙0≤t≤3.5﹚时,设△PCQ的面积为y(cm2)(当P、Q两点未开始运动时,△PCQ的面积为0).则y(cm2)和t﹙秒﹚的函数关系的图象大致是( )
的方向运动,速度为1cm/秒.当运动时间为t秒﹙0≤t≤3.5﹚时,设△PCQ的面积为y(cm2)(当P、Q两点未开始运动时,△PCQ的面积为0).则y(cm2)和t﹙秒﹚的函数关系的图象大致是( )

A.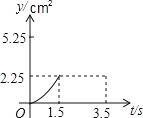 B.
B.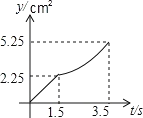 C.
C.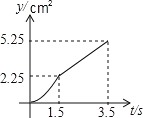 D.
D.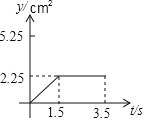
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲,乙,丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

(1)若运动员丙测试成绩的平均数和众数都是7,则成绩统计表中a= ,b= ;
(2)若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() ,
,![]() ,
,![]() )
)
(3)训练期间甲、乙、丙三人之间进行随机传球游戏,先由甲传出球,经过三次传球,球回到甲手中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
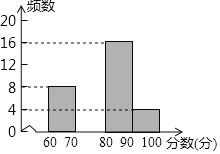
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
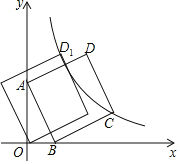
【题目】如图,直线AB与x的正半轴交于点B,且B(1,0),与y的正半轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=![]() (k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y=![]() (k≠0)上的点D1处,则k=_____.
(k≠0)上的点D1处,则k=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
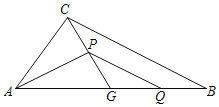
【题目】如图,在△ABC中,G为边AB中点,∠AGC=α.Q为线段BG上一动点(不与点B重合),点P在中线CG上,连接PA,PQ,记BQ=kGP.
(1)若α=60°,k=1,
①当BQ=![]() BG时,求∠PAG的度数.
BG时,求∠PAG的度数.
②写出线段PA、PQ的数量关系,并说明理由.
(2)当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com