
【题目】如图1,在ABCD中,E、F两点分别从A、D两点出发,以相同的速度在AD、DC边上匀速运动(E、F两点不与ABCD的顶点重合),连结BE、BF、EF.
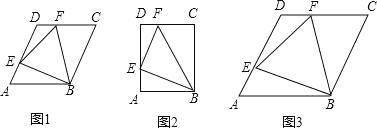
(1)如图2,当ABCD是矩形,AB=6,AD=8,∠BEF=90°时,求AE的长.
(2)如图2,当ABCD是菱形,且∠DAB=60°时,试判断△BEF的形状,并说明理由;
(3)如图3,在第(2)题的条件下,设菱形ABCD的边长为a,AE的长为x,试求△BEF面积y与x的函数关系式,并求出y的最小值.
【答案】(1)2;(2)等边三角形;(3)![]()
【解析】
试题分析:(1)依据矩形的性质可知∠D=∠A=90°,接下来,依据同角的余角相等可得到∠DFE=∠AEB,然后依据ASAS证明△DEF≌△ABE,依据全等三角形的性质可得到DE=6,从而可求得AE的长;
(2)连结BD.首先证明△ADB为等边三角形,于是得到BD=BC,然后再证明△BED≌△BFC,△AEB≌△DFB,由全等三角形的性质得到BE=BF,∠ABE=∠DBF,接下来证明∠EBF=60°,从而可判定△EBF为等边三角形.
(3)过点E作EM⊥AB,EN⊥DC,垂足为M、N,过点B作BG⊥DC,垂足为G.首先依据特殊锐角三角函数值可求得EM=![]() x,NE=
x,NE=![]() (a﹣x),BG=
(a﹣x),BG=![]() a,然后依据△EFB的面积=菱形的面积﹣△AEB的面积﹣△DFE的面积﹣△FCB的面积列出y与x的函数关系式,最后依据二次函数的性质求解即可.
a,然后依据△EFB的面积=菱形的面积﹣△AEB的面积﹣△DFE的面积﹣△FCB的面积列出y与x的函数关系式,最后依据二次函数的性质求解即可.
试题解析:(1)如图1所示:
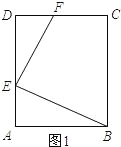
∵四边形ABCD为矩形,
∴∠D=∠A=90°.
∵∠BEF=90°,
∴∠DEF+∠AEB=90°.
又∵∠DEF+∠DFE=90°,
∴∠DFE=∠AEB.
在△DEF和△ABE中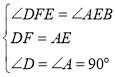 ,
,
∴△DEF≌△ABE.
∴AB=DE=6.
∴AE=AD﹣DE=8﹣6=2.
(2)如图2所示:连结BD.
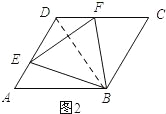
∵四边形ABCD为菱形,∠A=60°,
∴AD=AB=DC=BC,∠EDB=60°.
∵∠A=60°,AD=AB,
∴△ADB为等边三角形.
∴AD=AB=BD.
∴DB=BC.
∵AD=DC,AE=DF,
∴DE=FC.
在△BED和△BFC中,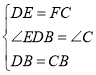 ,
,
∴△BED≌△BFC.
∴BE=BF.
在△AEB和△DFB中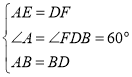 ,
,
∴△AEB≌△DFB.
∴∠ABE=∠DBF.
∴∠EBF=∠EBD+∠DBF=∠ABE+∠EBD=60°.
∴△EBF为等边三角形.
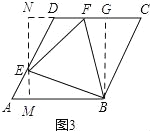
(3)如图3所示:过点E作EM⊥AB,EN⊥DC,垂足为M、N,过点B作BG⊥DC,垂足为G.
∵AE=DF=x,
∴DE=FC=a﹣x.
∵∠A=∠NDE=∠C=60°,
∴EM=![]() x,NE=
x,NE=![]() (a﹣x),BG=
(a﹣x),BG=![]() a.
a.
∵△EFB的面积=菱形的面积﹣△AEB的面积﹣△DFE的面积﹣△FCB的面积,
∴y=![]() a·a﹣
a·a﹣![]() a·
a·![]() x﹣
x﹣![]() ·x·
·x·![]() (a﹣x)﹣
(a﹣x)﹣![]() ·(a﹣x)·
·(a﹣x)·![]() a.
a.
∴y=![]() x2﹣
x2﹣![]() ax+
ax+![]() a2.
a2.
∴当x=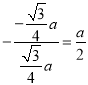 时,y取得最小值为
时,y取得最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)( ![]() )﹣1+(π﹣3)0+(﹣2)﹣2+|(﹣2)3|
)﹣1+(π﹣3)0+(﹣2)﹣2+|(﹣2)3|
(2)(9x3y﹣12xy3+3xy2)÷(﹣3xy)﹣(2y+x)(2y﹣x),其中x=1,y=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列线段中,能成比例的是( )
A. 3cm、6cm、8cm、9cmB. 3cm、5cm、6cm、9cm
C. 3cm、6cm、7cm、9cmD. 3cm、6cm、9cm、18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 过原点的直线都是正比例函数 B. 正比例函数图象经过原点
C. y=kx是正比例函数 D. y=3+x是正比例函数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线AC所在直线折叠,点D落在△ABC所在平面内的点E处.如果AE恰好经过BC的中点,那么ABCD的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计.两款运动鞋的销售量及总销售额如图所示:
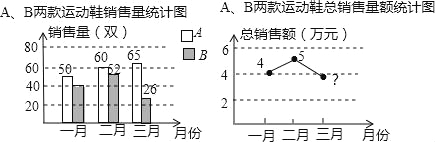
(1)一月份B款运动鞋的销售量是A款的![]() ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?
(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)综合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类且定价为15元的图书,书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠,学校如果多买12本,则可以享受优惠且所花钱数与原来相同,问学校获奖的同学有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com