
分析 根据相似三角形的性质得出相似比进而求出答案.
解答 解:∵一个三角形的三边长分别为$\sqrt{10}$,$\sqrt{5}$,2,与这个三角形相似的三角形有两边长分别为$\sqrt{2}$,$\frac{2}{5}$$\sqrt{5}$,
且$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$,$\frac{2}{\frac{2}{5}\sqrt{5}}$=$\sqrt{5}$,
∴设第三边长为x,
故$\frac{\sqrt{5}}{x}$=$\sqrt{5}$,
解得:x=1,
故第三边长为:1.
故答案为:1.
点评 此题主要考查了相似三角形的性质,正确得出对应边是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
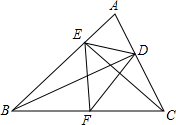 如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)
如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
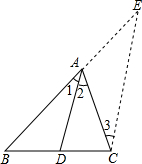 请阅读下面的材料,并回答所提出的问题.
请阅读下面的材料,并回答所提出的问题.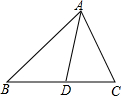
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com