
【题目】如图,点E是正方形ABCD的边AB上一点,将△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是______,旋转角的度数为______°.
(2)若∠DFB=65°,求∠DEB的度数.
(3)若AD=5,AE=m,求四边形DEBF的面积.

【答案】(1)点D,90;(2)∠DEB=115°;(3)25.
【解析】
(1)由已知可知,旋转中心为点D,旋转角∠ADC=90°;
(2)由旋转得:∠DEA=∠DFB=65°,则有∠DEB=180°-65°=115°;
(3)依题意得:△DCF的面积与△DAE的面积相等,所以四边形DEBF的面积与正方形ABCD的面积相等.
解:(1)由已知可知,旋转中心为点D,旋转角∠ADC=90°;
故答案为:点D,90;
(2)由旋转得:∠DEA=∠DFB=65°,
∴∠DEB=180°-65°=115°;
(3)依题意得:△DCF的面积与△DAE的面积相等,
∴四边形DEBF的面积与正方形ABCD的面积相等,
∴四边形DEBF的面积=25.


科目:初中数学 来源: 题型:
【题目】利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.你能利用数形结合的思想解决下列问题吗?



(1)如图①,一个边长为1的正方形,依次取正方形面积的![]() ,
,![]() ,
,![]() ,…,
,…, ![]() ,根据图示我们可以知道:
,根据图示我们可以知道: ![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() =________.(用含有n的式子表示)
=________.(用含有n的式子表示)
(2)如图②,一个边长为1的正方形,依次取剩余部分的![]() ,根据图示:
,根据图示:
计算: ![]() +
+![]() +
+![]() +…+
+…+![]() =________.(用含有n的式子表示)
=________.(用含有n的式子表示)
(3)如图③是一个边长为1的正方形,根据图示:
计算: ![]() +
+![]() +
+![]() +
+![]() +…+
+…+![]() =________.(用含有n的式子表示)
=________.(用含有n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意及解答过程填空:
如图所示,AB=10cm,D为AC的中点,DC=2cm,BE=![]() BC,求CE的长。
BC,求CE的长。
![]()
解:因为D为AC的中点,DC=2cm.
所以AC="_______DC=_______" cm.
由图可知:BC="______" -AC
="10" cm-____cm
=_______cm.
所以BE=![]() BC=______cm.
BC=______cm.
所以CE=BC-BE=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
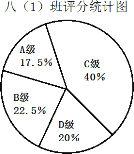

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°.
(1)直接填空:∠BAD=______°.
(2)点P在CD上,连结AP,AM平分∠DAP,AN平分∠PAB,AM、AN分别与射线BP交于点M、N.设∠DAM=α°.
①求∠BAN的度数(用含α的代数式表示).
②若AN⊥BM,试探究∠AMB的度数是否为定值?若为定值,请求出该定值;若不为定值,请用α的代数式表示它.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东昌湖举行的健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所滑行的路程y(m)与实践x(min)之间的函数关系如图所示,下列说法正确的有____________.

①乙队比甲队提前0. 25min到达终点.
②当乙队划行110m时,此时落后甲队15m.
③0. 5min后,乙队比甲队每分钟快40m.
④自1. 5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。

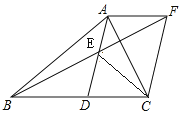
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com