
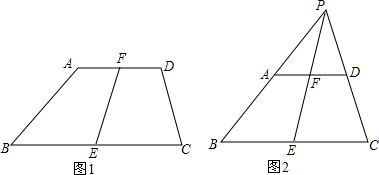
分析 假设直线AB、CD交于点P,直线AB、EF交于点P′.由AD∥BC,得出△PAD∽△PBC,根据相似三角形对应边成比例得出$\frac{PA}{PB}$=$\frac{AD}{BC}$,而AD=2AF,BC=2BE,那么$\frac{PA}{PB}$=$\frac{2AF}{2BE}$=$\frac{AF}{BE}$;由AF∥BE,得出△P′AF∽△P′BE,根据相似三角形对应边成比例得出$\frac{P′A}{P′B}$=$\frac{AF}{BE}$,等量代换得到$\frac{PA}{PB}$=$\frac{P′A}{P′B}$,根据比例的性质得出$\frac{PA}{AB}$=$\frac{P′A}{AB}$,又P、P′都在BA的延长线上,所以P、P′重合,从而证明直线AB、CD、EF交于一点P.
解答 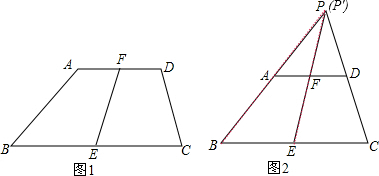 证明:如图,假设直线AB、CD交于点P,直线AB、EF交于点P′.
证明:如图,假设直线AB、CD交于点P,直线AB、EF交于点P′.
∵AD∥BC,
∴△PAD∽△PBC,
∴$\frac{PA}{PB}$=$\frac{AD}{BC}$,
∵AD=2AF,BC=2BE,
∴$\frac{PA}{PB}$=$\frac{2AF}{2BE}$=$\frac{AF}{BE}$;
∵AF∥BE,
∴△P′AF∽△P′BE,
∴$\frac{P′A}{P′B}$=$\frac{AF}{BE}$,
∴$\frac{PA}{PB}$=$\frac{P′A}{P′B}$,
∴$\frac{PA}{AB}$=$\frac{P′A}{AB}$,
又P、P′都在BA的延长线上,
∴P、P′重合,
∴直线AB、CD、EF交于一点P.
点评 本题考查了相似三角形的判定与性质,比例的性质,证明出$\frac{PA}{PB}$=$\frac{P′A}{P′B}$,再根据比例的性质得出$\frac{PA}{AB}$=$\frac{P′A}{AB}$是解题的关键.


科目:初中数学 来源: 题型:解答题
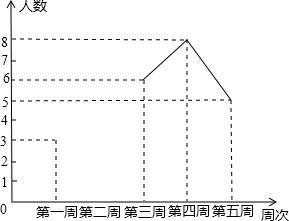 为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
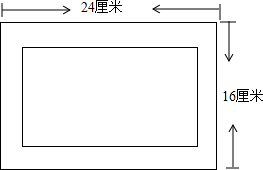 如图,相框的长为24厘米,宽为16厘米,外木缘制边框的宽相等,要使框内部分的面积是整个相框面积$\frac{1}{3}$,则边框的宽应为多少厘米?
如图,相框的长为24厘米,宽为16厘米,外木缘制边框的宽相等,要使框内部分的面积是整个相框面积$\frac{1}{3}$,则边框的宽应为多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解不等式$\frac{x-1}{3}≤5-x$,并把解集表示在数轴上.
(1)解不等式$\frac{x-1}{3}≤5-x$,并把解集表示在数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com