
°ĺŐ‚ńŅ°Ņ“—÷™Ň◊őÔŌŖy£Ĺax2+bx+c£®a°Ŕ0£©”Žx÷ŠĹĽ”ŕA£¨BŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ķ„BļÕĶ„CĶń◊ÝĪÍ∑÷Īūő™£®3£¨0£©°Ę£®0£¨©Ā3£©£¨Ň◊őÔŌŖĶń∂‘≥∆÷Šő™x£Ĺ1£¨Dő™Ň◊őÔŌŖĶń∂•Ķ„£ģ
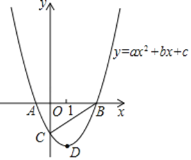
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£ģ
£®2£©Ķ„Eő™ŌŖ∂őBC…Ō“Ľ∂ĮĶ„£¨ĻżĶ„E◊ųx÷ŠĶńīĻŌŖ£¨”ŽŇ◊őÔŌŖĹĽ”ŕĶ„F£¨«ůňńĪŖ–őACFB√śĽżĶń◊Óīů÷Ķ£¨“‘ľįīň ĪĶ„EĶń◊ÝĪÍ£ģ
£®3£©Ň◊őÔŌŖĶń∂‘≥∆÷Š…Ō «∑Ůīś‘ŕ“ĽĶ„P£¨ Ļ°ųPCDő™Ķ»—Ł»żĹ«–ő£Ņ»Űīś‘ŕ£¨–ī≥ŲĶ„PĶ„Ķń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©y£Ĺx2©Ā2x©Ā3£Ľ£®2£©ňńĪŖ–őACFB√śĽżĶń◊Óīů÷Ķő™![]() £¨īň ĪĶ„EĶń◊ÝĪÍő™£®
£¨īň ĪĶ„EĶń◊ÝĪÍő™£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ£®3£©īś‘ŕ¬ķ◊„ŐűľĢĶńPĶ„£¨∆š◊ÝĪÍő™£®1£¨©Ā3£©ĽÚ£®1£¨©Ā2£©ĽÚ£®1£¨©Ā4+
£©£Ľ£®3£©īś‘ŕ¬ķ◊„ŐűľĢĶńPĶ„£¨∆š◊ÝĪÍő™£®1£¨©Ā3£©ĽÚ£®1£¨©Ā2£©ĽÚ£®1£¨©Ā4+![]() £©ĽÚ£®1£¨©Ā4©Ā
£©ĽÚ£®1£¨©Ā4©Ā![]() £©
£©
°ĺĹ‚őŲ°Ņ
£®1£©”…B°ĘCĶń◊ÝĪÍ£¨ĹŠļŌŇ◊őÔŌŖ∂‘≥∆÷Š£¨łýĺ›īż∂®ŌĶ ż∑®Ņ…«ůĶ√Ň◊őÔŌŖĹ‚őŲ Ĺ£Ľ
£®2£©”…B°ĘC◊ÝĪÍŅ…«ůĶ√÷ĪŌŖBCĹ‚őŲ Ĺ£¨…Ť≥ŲFĶ„◊ÝĪÍ£¨‘ÚŅ…ĪŪ ĺ≥ŲEĶ„◊ÝĪÍ£¨ī”∂ÝŅ…«ůĶ√EFĶń≥§£¨‘ÚŅ…ĪŪ ĺ≥Ų°ųCBFĶń√śĽż£¨ī”∂ÝŅ…ĪŪ ĺ≥ŲňńĪŖ–őACFBĶń√śĽż£¨‘ŔņŻ”√∂ĢīőļĮ żĶń–‘÷ Ņ…«ů∆š◊Óīů÷Ķ£¨ĹÝ∂Ý«ů≥ŲEĶ„Ķń◊ÝĪÍ£Ľ
£®3£©”…Ň◊őÔŌŖĹ‚őŲ ĹŅ…«ůĶ√DĶ„◊ÝĪÍ£¨Ņ……ŤPĶ„◊ÝĪÍő™£®1£¨t£©£¨‘ÚŅ…ĪŪ ĺ≥ŲPC°ĘPDļÕCDĶń≥§£¨”…Ķ»—Ł»żĹ«–őŅ…∑÷PC£ĹPD°ĘPC£ĹCDļÕPD£ĹCD»ż÷÷«ťŅŲ£¨∑÷ĪūĶ√ĶĹĻō”ŕtĶń∑Ĺ≥Ő£¨ľīŅ…«ůĶ√PĶ„◊ÝĪÍ£ģ
Ĺ‚£ļ£®1£©°ŖĶ„BļÕĶ„CĶń◊ÝĪÍ∑÷Īūő™£®3£¨0£©£®0£¨©Ā3£©£¨Ň◊őÔŌŖĶń∂‘≥∆÷Šő™x£Ĺ1£¨
°ŗ £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√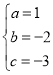 £¨
£¨
°ŗŇ◊őÔŌŖĹ‚őŲ Ĺő™y£Ĺx2©Ā2x©Ā3£Ľ
£®2£©£©…Ť÷ĪŌŖBCĹ‚őŲ Ĺő™y£Ĺkx+b£¨
īķ»ŽB£®3£¨0£©£¨C£®0£¨©Ā3£©Ķ√![]() £¨
£¨
Ĺ‚Ķ√£ļ![]() £¨
£¨
°ŗ÷ĪŌŖBCĹ‚őŲ Ĺő™y£Ĺx©Ā3£¨

°ŖEĶ„‘ŕ÷ĪŌŖBC…Ō£¨FĶ„‘ŕŇ◊őÔŌŖ…Ō£¨
°ŗ…ŤF£®x£¨x2©Ā2x©Ā3£©£¨E£®x£¨x©Ā3£©£¨
°ŖĶ„F‘ŕŌŖ∂őBCŌ¬∑Ĺ£¨
°ŗEF£Ĺx©Ā3©Ā£®x2©Ā2x©Ā3£©£Ĺ©Āx2+3x£¨
°ŗS°ųBCF£Ĺ![]() EFOB£Ĺ
EFOB£Ĺ![]() °Ń3£®©Āx2+3x£©£Ĺ©Ā
°Ń3£®©Āx2+3x£©£Ĺ©Ā![]() x2+
x2+![]() x£Ĺ©Ā
x£Ĺ©Ā![]() £®x©Ā
£®x©Ā![]() £©2+
£©2+![]() £¨
£¨
”÷°ŖS°ųABC£Ĺ![]() ABOC£Ĺ
ABOC£Ĺ![]() °Ń4°Ń3£Ĺ6£¨
°Ń4°Ń3£Ĺ6£¨
°ŗSňńĪŖ–őACFB£ĹS°ųABC+S°ųBCF£Ĺ6©Ā![]() £®x©Ā
£®x©Ā![]() £©2+
£©2+![]() £Ĺ©Ā
£Ĺ©Ā![]() £®x©Ā
£®x©Ā![]() £©2+
£©2+![]() £¨
£¨
°Ŗ©Ā![]() £ľ0£¨
£ľ0£¨
°ŗĶĪx£Ĺ![]() Ī£¨SňńĪŖ–őACFB”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™
Ī£¨SňńĪŖ–őACFB”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™![]() £¨īň ĪEĶ„◊ÝĪÍő™£®
£¨īň ĪEĶ„◊ÝĪÍő™£®![]() £¨©Ā
£¨©Ā![]() £©£¨
£©£¨
◊Ř…ŌŅ…Ķ√£ļňńĪŖ–őACFB√śĽżĶń◊Óīů÷Ķő™![]() £¨īň ĪĶ„EĶń◊ÝĪÍő™£®
£¨īň ĪĶ„EĶń◊ÝĪÍő™£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
£®3£©°Ŗy£Ĺx2©Ā2x©Ā3£Ĺ£®x©Ā1£©2©Ā4£¨
°ŗD£®1£¨©Ā4£©£¨«“C£®0£¨©Ā3£©£¨
°ŖPĶ„ő™Ň◊őÔŌŖ∂‘≥∆÷Š…ŌĶń“ĽĶ„£¨
°ŗ…ŤP£®1£¨t£©£¨
°ŗPC£Ĺ![]() £Ĺ
£Ĺ![]() £¨PD£Ĺ|t+4|£¨CD£Ĺ
£¨PD£Ĺ|t+4|£¨CD£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°Ŗ°ųPCDő™Ķ»—Ł»żĹ«–ő£¨
°ŗ∑÷PC£ĹPD°ĘPC£ĹCDļÕPD£ĹCD»ż÷÷«ťŅŲ£¨
ĘŔĶĪPC£ĹPD Ī£¨‘Ú![]() £Ĺ|t+4|£¨Ĺ‚Ķ√t£Ĺ©Ā3£¨
£Ĺ|t+4|£¨Ĺ‚Ķ√t£Ĺ©Ā3£¨
°ŗīň ĪPĶ„◊ÝĪÍő™£®1£¨©Ā3£©£Ľ
ĘŕĶĪPC£ĹCD Ī£¨‘Ú![]() £Ĺ
£Ĺ![]() £¨Ĺ‚Ķ√t£Ĺ©Ā2ĽÚt£Ĺ©Ā4£®”ŽDĶ„÷ōļŌ£¨…Š»•£©£¨
£¨Ĺ‚Ķ√t£Ĺ©Ā2ĽÚt£Ĺ©Ā4£®”ŽDĶ„÷ōļŌ£¨…Š»•£©£¨
°ŗīň ĪPĶ„◊ÝĪÍő™£®1£¨©Ā2£©£Ľ
ĘŘĶĪPD£ĹCD Ī£¨‘Ú|t+4|£Ĺ![]() £¨Ĺ‚Ķ√t£Ĺ©Ā4+
£¨Ĺ‚Ķ√t£Ĺ©Ā4+![]() ĽÚt£Ĺ©Ā4©Ā
ĽÚt£Ĺ©Ā4©Ā![]() £¨
£¨
°ŗīň ĪPĶ„◊ÝĪÍő™£®1£¨©Ā4+![]() £©ĽÚ£®1£¨©Ā4©Ā
£©ĽÚ£®1£¨©Ā4©Ā![]() £©£Ľ
£©£Ľ
◊Ř…ŌŅ…÷™£¨īś‘ŕ¬ķ◊„ŐűľĢĶńPĶ„£¨∆š◊ÝĪÍő™£®1£¨©Ā3£©ĽÚ£®1£¨©Ā2£©ĽÚ£®1£¨©Ā4+![]() £©ĽÚ£®1£¨©Ā4©Ā
£©ĽÚ£®1£¨©Ā4©Ā![]() £©£ģ
£©£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨Ň◊őÔŌŖ![]() ”Ž
”Ž![]() ÷ŠĹĽ”ŕ
÷ŠĹĽ”ŕ![]() ŃĹĶ„£¨”Ž
ŃĹĶ„£¨”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() £¨
£¨![]() £¨ĺō–ő
£¨ĺō–ő![]() ĶńĪŖ
ĶńĪŖ![]() £¨—”≥§
£¨—”≥§![]() ĹĽŇ◊őÔŌŖ”ŕĶ„
ĹĽŇ◊őÔŌŖ”ŕĶ„![]() .
.
£®1£©«ůŇ◊őÔŌŖĶńĪŪīÔ Ĺ£Ľ
£®2£©»ÁÕľ2£¨Ķ„![]() «÷ĪŌŖ
«÷ĪŌŖ![]() …Ō∑ĹŇ◊őÔŌŖ…ŌĶń“ĽłŲ∂ĮĶ„£¨ĻżĶ„
…Ō∑ĹŇ◊őÔŌŖ…ŌĶń“ĽłŲ∂ĮĶ„£¨ĻżĶ„![]() ◊ų
◊ų![]() ÷ŠĶń∆Ĺ––ŌŖĹĽ÷ĪŌŖ
÷ŠĶń∆Ĺ––ŌŖĹĽ÷ĪŌŖ![]() ”ŕĶ„
”ŕĶ„![]() £¨◊ų
£¨◊ų![]() £¨īĻ◊„ő™
£¨īĻ◊„ő™![]() .…Ť
.…Ť![]() Ķń≥§ő™
Ķń≥§ő™![]() £¨Ķ„
£¨Ķ„![]() ĶńļŠ◊ÝĪÍő™
ĶńļŠ◊ÝĪÍő™![]() £¨«ů
£¨«ů![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ «£®≤ĽĪō–ī≥Ų
ĶńļĮ żĻōŌĶ «£®≤ĽĪō–ī≥Ų![]() Ķń»°÷Ķ∑∂őߣ©£¨≤Ę«ů≥Ų
Ķń»°÷Ķ∑∂őߣ©£¨≤Ę«ů≥Ų![]() Ķń◊Óīů÷Ķ£Ľ
Ķń◊Óīů÷Ķ£Ľ
£®3£©»ÁĻŻĶ„![]() «Ň◊őÔŌŖ∂‘≥∆÷Š…ŌĶń“ĽĶ„£¨Ň◊őÔŌŖ…Ō «∑Ůīś‘ŕĶ„
«Ň◊őÔŌŖ∂‘≥∆÷Š…ŌĶń“ĽĶ„£¨Ň◊őÔŌŖ…Ō «∑Ůīś‘ŕĶ„![]() £¨ ĻĶ√“‘
£¨ ĻĶ√“‘![]() ő™∂•Ķ„ĶńňńĪŖ–ő «∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ£¨÷ĪĹ”–ī≥Ųňý”–¬ķ◊„ŐűľĢĶń
ő™∂•Ķ„ĶńňńĪŖ–ő «∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ£¨÷ĪĹ”–ī≥Ųňý”–¬ķ◊„ŐűľĢĶń![]() Ķń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
Ķń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ“ĽłŲ≤ĽÕł√ųĶńīŁ◊”÷–◊į”–īů–°°Ę–ő◊īÕÍ»ęŌŗÕ¨Ķń»żłŲ–°«Ú£¨…Ō√ś∑÷ĪūĪÍ”–1£¨2£¨3»żłŲ ż◊÷£ģ
£®1£©ī”÷–ňśĽķ√Ģ≥Ų“ĽłŲ«Ú£¨«ů’‚łŲ«Ú…Ō ż◊÷ «∆ś żĶńłŇ¬ « £Ľ
£®2£©ī”÷–Ō»ňśĽķ√Ģ≥Ų“ĽłŲ«Úľ«Ō¬«Ú…Ō ż◊÷£¨»Ľļů∑ŇĽōŌī‘»£¨Ĺ”◊Ň‘ŔňśĽķ√Ģ≥Ų“ĽłŲ£¨«ů’‚ŃĹłŲ«Ú…ŌĶń ż∂ľ «∆ś żĶńłŇ¬ £®”√Ń–ĪŪĽÚ ų◊īÕľ∑Ĺ∑®£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™£ļ»ÁÕľ£¨![]() «°—
«°—![]() Ķń÷Īĺ∂£¨
Ķń÷Īĺ∂£¨![]() ő™°—
ő™°—![]() Õ‚“ĽĶ„£¨
Õ‚“ĽĶ„£¨![]() £¨īĻ◊„ő™
£¨īĻ◊„ő™![]() £¨Ō“
£¨Ō“![]() £¨«“
£¨«“![]() £¨
£¨![]() £ģ
£ģ
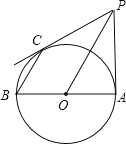
£®1£©«ů÷§£ļ![]() «°—
«°—![]() Ķń«–ŌŖ£Ľ
Ķń«–ŌŖ£Ľ
£®2£©«ů°—![]() ĶńįŽĺ∂£ģ
ĶńįŽĺ∂£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ķ„A «Ň◊őÔŌŖ![]() ∂‘≥∆÷Š…ŌĶń“ĽĶ„£¨Ń¨Ĺ”OA£¨“‘Aő™–ż◊™÷––ńĹęAOńś Ī’Ž–ż◊™90°„Ķ√ĶĹAO°š£¨ĶĪO°š«°ļ√¬š‘ŕŇ◊őÔŌŖ…Ō Ī£¨Ķ„AĶń◊ÝĪÍő™______________£ģ
∂‘≥∆÷Š…ŌĶń“ĽĶ„£¨Ń¨Ĺ”OA£¨“‘Aő™–ż◊™÷––ńĹęAOńś Ī’Ž–ż◊™90°„Ķ√ĶĹAO°š£¨ĶĪO°š«°ļ√¬š‘ŕŇ◊őÔŌŖ…Ō Ī£¨Ķ„AĶń◊ÝĪÍő™______________£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ“ĽłŲ≤ĽÕł√ųĶńīŁ◊”÷–◊į”–≥ż—’…ęÕ‚∆š”ŗĺýŌŗÕ¨ĶńmłŲ–°«Ú£¨∆š÷– 5 łŲļŕ«Ú£¨ ī”īŁ÷–ňśĽķ√Ģ≥Ų“Ľ«Ú£¨ľ«Ō¬∆š—’…ę£¨’‚≥∆ő™“ņīő√Ģ«Ú ‘—ť£¨÷ģļůį—ňŁ∑ŇĽōīŁ ÷–£¨ĹŃ‘»ļů£¨‘ŔľŐ–Ý√Ģ≥Ų“Ľ«Ú£ģ“‘Ō¬ «ņŻ”√ľ∆ň„Ľķń£ń‚Ķń√Ģ«Ú ‘—ťīő ż”Ž√Ģ≥Ųļŕ«Úīő żĶńŃ–ĪŪ£ļ
√Ģ«Ú ‘—ťīő ż | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
√Ģ≥Ųļŕ«Úīő ż | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
łýĺ›Ń–ĪŪ£¨Ņ…“‘Ļņľ∆≥Ų m Ķń÷Ķ «£® £©
A. 5 B. 10 C. 15 D. 20
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() ”ŕ
”ŕ![]() £¨
£¨![]() £¨
£¨![]() ő™
ő™![]() ĪŖ…Ō“ĽĶ„£ģ
ĪŖ…Ō“ĽĶ„£ģ
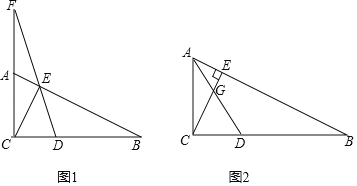
£®1£©ĶĪ![]() Ī£¨÷ĪĹ”–ī≥Ų
Ī£¨÷ĪĹ”–ī≥Ų![]() °°°°£¨
°°°°£¨![]() °°°°£ģ
°°°°£ģ
£®2£©»ÁÕľ1£¨ĶĪ![]() £¨
£¨![]() Ī£¨Ń¨
Ī£¨Ń¨![]() ≤Ę—”≥§ĹĽ
≤Ę—”≥§ĹĽ![]() —”≥§ŌŖ”ŕ
—”≥§ŌŖ”ŕ![]() £¨«ů÷§£ļ
£¨«ů÷§£ļ![]() £ģ
£ģ
£®3£©»ÁÕľ2£¨Ń¨![]() ĹĽ
ĹĽ![]() ”ŕ
”ŕ![]() £¨ĶĪ
£¨ĶĪ![]() «“
«“![]() Ī£¨«ů
Ī£¨«ů![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ£®8∑÷£©»ÁÕľ£¨“—÷™O «◊ÝĪÍ‘≠Ķ„£¨B°ĘCŃĹĶ„Ķń◊ÝĪÍ∑÷Īūő™£®3£¨£≠1£©°Ę£®2£¨1£©°£

£®1£©“‘OĶ„ő™őĽň∆÷––ń‘ŕy÷ŠĶń◊ů≤ŗĹę°ųOBC∑ŇīůĶĹŃĹĪ∂Ľ≠≥ŲÕľ–ő°£
£®2£©–ī≥ŲB°ĘCŃĹĶ„Ķń∂‘”¶Ķ„B°ĘCĶń◊ÝĪÍ£Ľ
£®3£©»ÁĻŻ°ųOBCńŕ≤Ņ“ĽĶ„MĶń◊ÝĪÍő™(x£¨y)£¨–ī≥ŲMĶń∂‘”¶Ķ„MĶń◊ÝĪÍ°£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“ĽīőļĮ ż![]() ĶńÕľŌů”Ž∑īĪ»ņżļĮ ż
ĶńÕľŌů”Ž∑īĪ»ņżļĮ ż![]() ĶńÕľŌůŌŗĹĽ”ŕA£®2£¨1£©£¨BŃĹĶ„£ģ
ĶńÕľŌůŌŗĹĽ”ŕA£®2£¨1£©£¨BŃĹĶ„£ģ

£®1£©«ů≥Ų∑īĪ»ņżļĮ ż”Ž“ĽīőļĮ żĶńĪŪīÔ Ĺ£Ľ
£®2£©«Ž÷ĪĹ”–ī≥ŲBĶ„Ķń◊ÝĪÍ£¨≤Ę÷ł≥Ų Ļ∑īĪ»ņżļĮ ż÷Ķīů”ŕ“ĽīőļĮ ż÷ĶĶńxĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com