
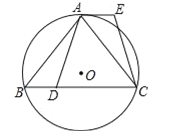
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据等弧所对的圆周角相等,得出∠B=∠ACB,再根据全等三角形的判定得△ABD≌△CAE,即可得出AD=CE;
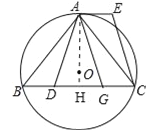
(2)连接AO并延长,交边BC于点H,由等腰三角形的性质和外心的性质得出AH⊥BC,再由垂径定理得BH=CH,得出CG与AE平行且相等.
试题解析:(1)在⊙O中,∵![]() ,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
(2)连接AO并延长,交边BC于点H,∵![]() ,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.
,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.


科目:初中数学 来源: 题型:
【题目】将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°.
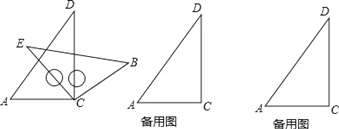
(1)求证:∠ACE=∠BCD;
(2)猜想∠ACB与∠ECD数量关系并说明理由;
(3)按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 135° B. 130° C. 125°
D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年全国国民生产总值约为74 000 000 000 000元,比上年增长6.7%,将74 000 000 000 000元用科学计数法表示为( )元
A.0.74×1014
B.7.4×1013
C.74×1012
D.7.40×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲型H1N1流感确诊病例需需住院隔离观察,医生要要掌握患者在一周内的体温是否稳定,则医生需了解患者7天体温的( ).
A. 众数B. 方差C. 平均数D. 频数
查看答案和解析>>
科目:初中数学 来源: 题型:
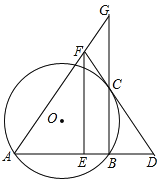
【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于点C,过C作⊙O的切线交AB的延长线于点D,取AD的中点E,过E作EF∥BC交DC 的延长线与点F,连接AF并延长交BC的延长线于点G.
求证:(1)FC=FG (2)![]() =BCCG.
=BCCG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对单项式“5x”,我们可以这样来解释:某人以5千米/小时的速度走了x小时,他一共走的路程是5x千米,请你对“5x”再给出另一个生活实际方面的解释_________________________________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com