
【题目】将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°.
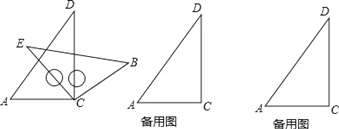
(1)求证:∠ACE=∠BCD;
(2)猜想∠ACB与∠ECD数量关系并说明理由;
(3)按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
【答案】(1)证明见解析;(2)猜想:∠ACB+∠ECD=180°.理由见解析;(3)当∠ACB=120°或60°时,AD∥CB.理由理由见解析.
【解析】试题分析:
(1)由∠ACD=∠BCE=90°,可得∠ACD-∠DCE=∠BCE-∠DCE,从而可得∠ACE=∠BCD;
(2)猜想:∠ACB+∠ECD=180°.由∠ACB+∠ECD=∠ACD+∠BCD+∠ECD=∠ACD+∠BCE=90°+90°=180°可得结论;
(3)如下图,因为∠A=60°,根据“同旁内角互补,两直线平行和内错角相等,两直线平行”可知,当∠ACB=120°,或∠ACB=60°时,AD∥BC.
试题解析:
(1)∵∠ACD=∠ECB=90°,
∴∠ACD﹣∠ECD=∠ECB﹣∠ECD,
即∠ACE=∠BCD.
(2)猜想:∠ACB+∠ECD=180°.理由如下:
∵∠ACB=∠ACD+∠DCB
∴∠ACB+∠ECD
=∠ACD+∠DCB+∠ECD
又∵∠DCB+∠ECD=∠ECB,
∴∠ACB+∠ECD=∠ACD+∠ECB=90°+90°=180°.
(3)当∠ACB=120°或60°时,AD∥CB.理由如下:
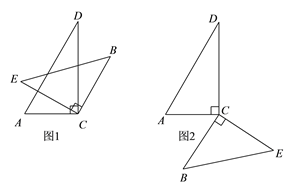
①如图1,根据“同旁内角互补,两直线平行”:
当∠A+∠ACB=180°时,AD∥BC,
此时,∠ACB=180°﹣∠A=180°﹣60°=120°.
②如图2,根据“内错角相等,两直线平行”:
当∠ACB=∠A=60°时,AD∥BC.
综上所述,当∠ACB=120°或60°时,AD∥BC.


科目:初中数学 来源: 题型:
【题目】已知y与x-3成正比例,当x=4时,y=3.
(1) 求出y与x之间的函数关系式;
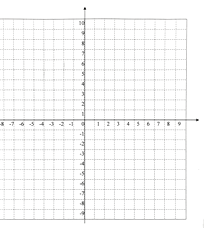
(2) y与x之间是什么函数关系? 并在平面直角坐标系中画出该函数的图像;
(3) 当x=2.5时,y的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
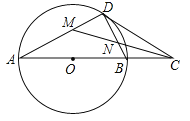
【题目】如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.
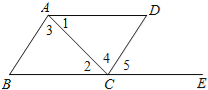
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
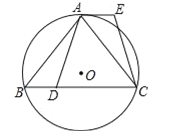
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com