
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
【答案】1
【解析】试题分析:
根据数轴上数的排布规律,可以得到a与b的值. 根据倒数的定义,可以得到c与d的乘积cd的值. 根据相反数的性质,可以得到m+n的值. 根据有理数的相关概念,可以得到y的值. 先将a,b,cd,y的值代入待求值的代数式,进行运算后发现运算结果中含有m+n. 将m+n的值代入该运算结果,进一步运算即可得到要求的值.
试题解析:
因为在数轴上表示数a的点在原点左侧,所以a是负数.
因为在数轴上表示数a的点距离原点3个单位长,所以![]() .
.
因此,a=-3.
因为在数轴上表示数b的点在原点右侧,所以b是正数.
因为在数轴上表示数b的点距离原点2个单位长,所以![]() .
.
因此,b=2.
因为c和d互为倒数,所以cd=1.
因为m与n互为相反数,所以m+n=0.
因为y为最大的负整数,所以y=-1.
将a=-3,b=2,cd=1,y=-1代入(y+b)2+m(a-cd)-nb2,得
![]()
=![]()
=![]() ,
,
将m+n=0代入上式,得
![]() =
=![]() =1.
=1.
综上所述,在本题的条件下,(y+b)2+m(a-cd)-nb2的值为1.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】问题提出
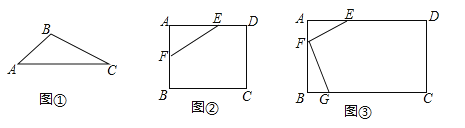
(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
问题探究
(2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决
(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD.AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD.AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标. 
查看答案和解析>>
科目:初中数学 来源: 题型:
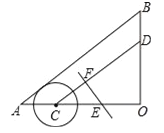
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了 s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一栋5层的教学大楼,第一层没有教室,二至五层,每层楼有6间教室,进出这栋大楼共有两道大小相同的大门和一道小门(平时小门不开).安全检查中,对这3道门进行了测试:当同时开启一道大门和一道小门时,3分钟内可以通过540名学生,若一道大门平均每分钟比一道小门可多通过60名学生.
(1)求平均每分钟一道大门和一道小门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内安全撤离.这栋教学大楼每间教室平均有45名学生,问:在紧急情况下只开启两道大门是否可行?为什么?3道门都开启呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
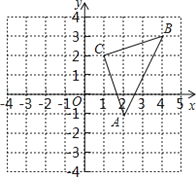
【题目】平面直角坐标系中,三角形ABC的顶点都在网格点上。
(1)平移三角形ABC,使点C与坐标原点O是对应点,请画出平移后的三角形A′B′C′;
(2)写出A、B两点的对应点A′、B′的坐标;
(3)求出三角形ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°.
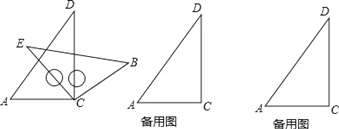
(1)求证:∠ACE=∠BCD;
(2)猜想∠ACB与∠ECD数量关系并说明理由;
(3)按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com