
【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标. 
【答案】(1)a=-4,b=2;(2)点C的坐标为(0,4)或(0,-4);(3)点P沿x轴负半轴方向以每秒1个单位长度平移至点Q,点Q的坐标为(-4,3).
【解析】试题分析:(1)根据二次根式与绝对值的非负性可得a+4=0,b-2=0,解得a=-4,b=2;
(2)设点C到x轴的距离为h,利用三角形的面积公式可解得h=4,要考虑点C在y轴正半轴与负半轴两种情况;
(3)先根据四边形ABPQ的面积积S=![]() (6+PQ)×3=15解得PQ=4,再求得点Q的坐标为(-4,3).
(6+PQ)×3=15解得PQ=4,再求得点Q的坐标为(-4,3).
试题解析:(1)根据题意,得
a+4=0,b-2=0,
解得a=-4,b=2;
(2)存在.设点C到x轴的距离为h,
则S△ABC=![]() ABh=
ABh=![]() ×6h=12解得h=4,
×6h=12解得h=4,
所以点C的坐标为(0,4)或(0,-4);
(3)四边形ABPQ的面积S=![]() (6+PQ)×3=15解得PQ=4.
(6+PQ)×3=15解得PQ=4.
点P沿x轴负半轴方向以每秒1个单位长度平移至点Q,所以点Q的坐标为(-4,3).


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.
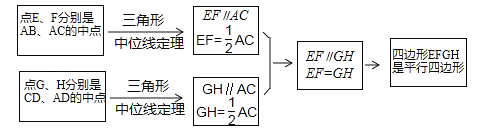
结合小敏的思路作答
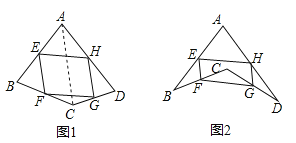
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x-3成正比例,当x=4时,y=3.
(1) 求出y与x之间的函数关系式;
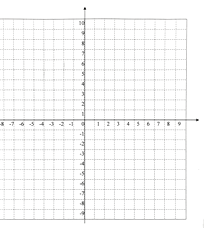
(2) y与x之间是什么函数关系? 并在平面直角坐标系中画出该函数的图像;
(3) 当x=2.5时,y的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
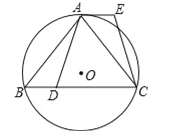
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com