
【题目】问题提出
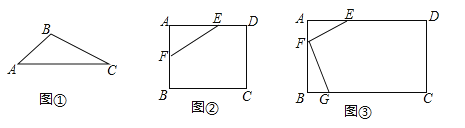
(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
问题探究
(2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决
(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD.AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD.AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
【答案】(1)作图见解析;(2)存在,最小值为![]() ;(3)能,
;(3)能,![]() .
.
【解析】
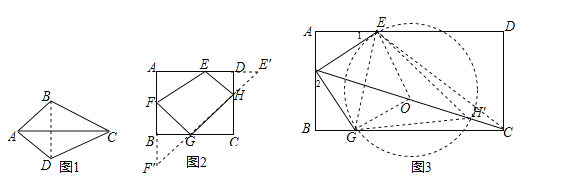
试题分析:(1)作B关于AC 的对称点D,连接AD,CD,△ACD即为所求;
(2)作E关于CD的对称点E′,作F关于BC的对称点F′,连接E′F′,得到此时四边形EFGH的周长最小,根据轴对称的性质得到BF′=BF=AF=2,DE′=DE=2,∠A=90°,于是得到AF′=6,AE′=8,求出E′F′=10,EF=![]() 即可得到结论;
即可得到结论;
(3)根据余角的性质得到1=∠2,推出△AEF≌△BGF,根据全等三角形的性质得到AF=BG,AE=BF,设AF=x,则AE=BF=3﹣x根据勾股定理列方程得到AF=BG=1,BF=AE=2,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°,以O为圆心,以EG为半径作⊙O,则∠EHG=45°的点在⊙O上,连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′GH′,则∠EH′G=45°,于是得到四边形EFGH′是符合条件的最大部件,根据矩形的面积公式即可得到结论.
试题解析:(1)如图1,△ADC即为所求;
(2)存在,理由:作E关于CD的对称点E′,作F关于BC的对称点F′,连接E′F′,交BC于G,交CD于H,连接FG,EH,则F′G=FG,E′H=EH,则此时四边形EFGH的周长最小,由题意得:BF′=BF=AF=2,DE′=DE=2,∠A=90°,∴AF′=6,AE′=8,∴E′F′=10,EF=![]() ,∴四边形EFGH的周长的最小值=EF+FG+GH+HE=EF+E′F′=
,∴四边形EFGH的周长的最小值=EF+FG+GH+HE=EF+E′F′=![]() ,∴在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小,最小值为
,∴在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小,最小值为![]() ;
;
(3)能裁得,理由:∵EF=FG=![]() ,∠A=∠B=90°,∠1+∠AFE=∠2+AFE=90°,∴∠1=∠2,在△AEF与△BGF中,∵∠1=∠2,∠A=∠B,EF=FG,∴△AEF≌△BGF,∴AF=BG,AE=BF,设AF=x,则AE=BF=3﹣x,∴
,∠A=∠B=90°,∠1+∠AFE=∠2+AFE=90°,∴∠1=∠2,在△AEF与△BGF中,∵∠1=∠2,∠A=∠B,EF=FG,∴△AEF≌△BGF,∴AF=BG,AE=BF,设AF=x,则AE=BF=3﹣x,∴![]() ,解得:x=1,x=2(不合题意,舍去),∴AF=BG=1,BF=AE=2,∴DE=4,CG=5,连接EG,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°,以O为圆心,以EG为半径作⊙O,则∠EHG=45°的点在⊙O上,连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′GH′,则∠EH′G=45°,此时,四边形EFGH′是要想裁得符合要求的面积最大的,∴C在线段EG的垂直平分线设,∴点F,O,H′,C在一条直线上,∵EG=
,解得:x=1,x=2(不合题意,舍去),∴AF=BG=1,BF=AE=2,∴DE=4,CG=5,连接EG,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°,以O为圆心,以EG为半径作⊙O,则∠EHG=45°的点在⊙O上,连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′GH′,则∠EH′G=45°,此时,四边形EFGH′是要想裁得符合要求的面积最大的,∴C在线段EG的垂直平分线设,∴点F,O,H′,C在一条直线上,∵EG=![]() ,∴OF=EG=
,∴OF=EG=![]() ,∵CF=
,∵CF=![]() ,∴OC=
,∴OC=![]() ,∵OH′=OE=FG=
,∵OH′=OE=FG=![]() ,∴OH′<OC,∴点H′在矩形ABCD的内部,∴可以在矩形ABCD中,裁得符合条件的面积最大的四边形EFGH′部件,这个部件的面积=
,∴OH′<OC,∴点H′在矩形ABCD的内部,∴可以在矩形ABCD中,裁得符合条件的面积最大的四边形EFGH′部件,这个部件的面积=![]() EGFH′=
EGFH′=![]() =
=![]() ,∴当所裁得的四边形部件为四边形EFGH′时,裁得了符合条件的最大部件,这个部件的面积为(
,∴当所裁得的四边形部件为四边形EFGH′时,裁得了符合条件的最大部件,这个部件的面积为(![]() )m2.
)m2.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】下列事件中,必然发生的是( )
A. 某射击运动射击一次,命中靶心
B. 掷一次骰子,向上的一面是6点
C. 通常情况下,水加热到100℃时沸腾
D. 抛一枚硬币,落地后正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:
 观察由※组成的图案和算式,解答问题:
观察由※组成的图案和算式,解答问题:
1+3=4=![]()
1+3+5=9=![]()
1+3+5+7=16=![]()
1+3+5+7+9=25=![]()
(1)请猜想1+3+5+7+9+ … +29= ;(3分)
(2)请猜想1+3+5+7+9+ … +(2n-1)+(2n+1)= ;(3分)
(3)请用上述规律计算:(6分)41+43+45+ …… +77+79
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
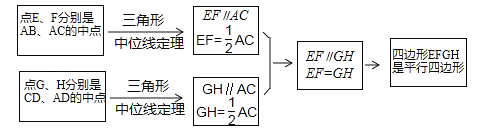
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.
结合小敏的思路作答
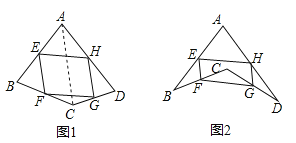
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 有理数分为正数和负数 B. 符号不同的两个数互为相反数
C. 所有的有理数都能用数轴上的点表示 D. 两数相加,和一定大于任何一个数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x-3成正比例,当x=4时,y=3.
(1) 求出y与x之间的函数关系式;
(2) y与x之间是什么函数关系? 并在平面直角坐标系中画出该函数的图像;
(3) 当x=2.5时,y的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com