练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】用反证法证明“一个三角形中至多有一个钝角”时，应假设 ．

    【答案】三角形中至少有两个是钝角．

    【解析】

    用反证法证明的第一步就是作出与原命题相矛盾的假设，

    解：根据反证法就是从结论的反面出发进行假设，
    ∴证明“一个三角形中至多有一个钝角”，应假设：一个三角形中至少有两个钝角．
    故答案为一个三角形中至少有两个钝角

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一次函数，回答下列问题：

    （1）若次函数的图像过原点，求k的值；

    （2）无论k取何值，该函数的图像总经过一个定点，请你求出这个定点的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 “对顶角相等”的逆命题是 ______________________________________________________，该逆命题是 ___________命题

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1和图2，∠ACB=90°，AC=BC，BD⊥DE，AE⊥DE，足分别为D、E．


    （1）图1中，证明：△ACE≌△CBD；

    （2）图2中，若AE=2，BD=4，计算DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

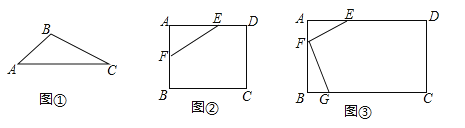
    【题目】问题提出

    （1）如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．

    问题探究

    （2）如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．

    问题解决

    （3）如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG=米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD．AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠AOB=，P为∠AOB内部一点，点P关于OA、OB的对称点分别为P1、P2，则△OP1P2是_______________三角形；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平行四边形的面积等于的积;过平行四边形对角线的的任一直线都将平行四边形分成面积相等的两部分.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某巡警骑摩托车在一条南北大道上巡逻，某天他从岗亭出发，晚上停留在A处，规定向北方向为正，当天行驶情况记录如下（单位：千米）：+10，﹣8，+7，﹣15，+6，﹣16，+4，﹣2

    （1）A处在岗亭何方？距离岗亭多远？

    （2）若摩托车每行驶1千米耗油0.5升，这一天共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校一栋5层的教学大楼，第一层没有教室，二至五层，每层楼有6间教室，进出这栋大楼共有两道大小相同的大门和一道小门（平时小门不开）．安全检查中，对这3道门进行了测试：当同时开启一道大门和一道小门时，3分钟内可以通过540名学生，若一道大门平均每分钟比一道小门可多通过60名学生．

    （1）求平均每分钟一道大门和一道小门各可以通过多少名学生？

    （2）检查中发现，紧急情况时因学生拥挤，出门的效率降低20%．安全检查规定：在紧急情况下全大楼的学生应在5分钟内安全撤离．这栋教学大楼每间教室平均有45名学生，问：在紧急情况下只开启两道大门是否可行？为什么？3道门都开启呢？

    查看答案和解析>>

    同步练习册答案