
【题目】如图1和图2,∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,足分别为D、E.


(1)图1中,证明:△ACE≌△CBD;
(2)图2中,若AE=2,BD=4,计算DE的长.
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)如图1,根据垂直的定义和同角的余角相等得到∠E=∠D=90°,∠1=∠2,则结合已知条件AC=BC由AAS证得:△ACE≌△CBD;
(2)如图2,同(1),证得△ACE≌△CBD,则根据全等三角形的对应边相等推知:CE=BD=4,AE=CD=2,故DE=CE-CD=4-2=2.
试题解析:(1)证明:如图1,
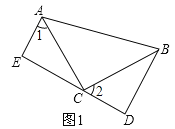
∵BD⊥DE,AE⊥DE,
∴∠E=∠D=90°.
又∵∠ACB=90°,
∴∠1=∠2,
∴在△ACE与△CBD中,

∴△ACE≌△CBD(AAS);
(2)如图2,
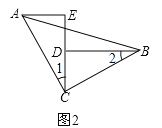
同(1),证得△ACE≌△CBD,则
∴CE=BD=4,AE=CD=2,
∴DE=CE-CD=4-2=2.


科目:初中数学 来源: 题型:
【题目】某铁工艺品商城某天销售了110件工艺品,其统计如表:
货种 | A | B | C | D | E |
销售量(件) | 10 | 40 | 30 | 10 | 20 |
该店长如果想要了解哪个货种的销售量最大,那么他应该关注的统计量是( )
A.平均数B.众数C.中位数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M向左平移4个单位长度后的坐标为(-1,2),则点M原来的坐标为( )
A.(-5,2)B.(3,2)C.(-1,6)D.(-1,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2m,宽为2n的长方形,沿图a中虚线用剪刀把它均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)请用两种不同的方法求图b中阴影部分的面积:
方法1: ____ (只列式,不化简)
方法2: ______ (只列式,不化简)
(2)观察图b,写出代数式(m+n)2,(m-n)2,mn之间的等量关系: ______ ;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=7,ab=5,
则(a-b)2= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.
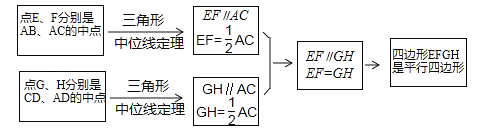
结合小敏的思路作答
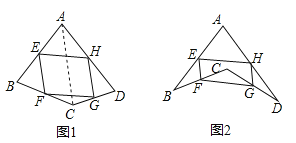
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是( )
A.0.1
B.0.2
C.0.3
D.0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
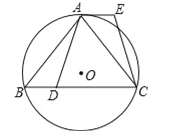
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com