
【题目】甲开车从距离B市100千米的A市出发去B市,乙从同一路线上的C市出发也去往B.市,二人离A市的距离与行驶时间的函数图像如图所示(y代表距离,x代表时间)
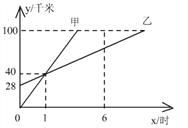
(1)C市离A市的距离是_________千米;
(2)甲的速度是________千米∕小时,乙的速度是___________千米∕小时;
(3)________小时,甲追上乙;
(4)试分别写出甲、乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式.
【答案】(1)28;(2)40,12;(3)1;(4)甲:y=40x,乙:y=12x+28.
【解析】
(1)由函数图象可以直接得出C市离A市的距离是28千米;
(2)由函数图象可以直接得出甲的速度为40千米∕小时,乙的速度为12千米∕小时;(3)由函数图象可以直接得出1小时,甲追上乙;
(4)设甲离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为y甲=![]() x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为y乙=
x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为y乙=![]() x+b,由待定系数法求出其解即可.
x+b,由待定系数法求出其解即可.
解:(1)由函数图象可以直接得出C市离A市的距离是28千米.
故答案为28;
(2)由函数图象可以直接得出甲的速度为40千米∕小时,乙的速度为12千米∕小时.
故答案为40,12;
(3)由函数图象可以直接得出1小时,甲追上乙.
故答案为1;
(4)设甲离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为:![]() =
=![]() x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为:
x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为:![]() =
=![]() x+b,由题意,得40=
x+b,由题意,得40=![]() ,∴
,∴![]() =40x(0≤x≤2.5) .
=40x(0≤x≤2.5) .
由![]() ,解得:
,解得:![]() ,
,
∴![]() =12x+28(0≤x≤6) .
=12x+28(0≤x≤6) .


科目:初中数学 来源: 题型:
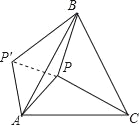
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
出厂价 | 成本价 | 排污处理费 | |
甲种塑料 | 2100(元/吨) | 800(元/吨) | 200(元/吨) |
乙种塑料 | 2400(元/吨) | 1100(元/吨) | 100(元/吨) 另每月还需支付设备管理、维护费20000元 |
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
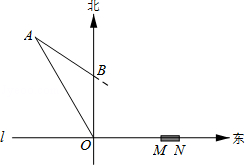
【题目】如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距![]() 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.

(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com