
如图,经过点A(0,﹣6)的抛物线 与x轴相交于B(﹣2,0),C两点.
与x轴相交于B(﹣2,0),C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(3)在(2)的结论下,新抛物线y1上是否存在点Q,使得△QAB是以AB为底边的等腰三角形?请分析所有可能出现的情况,并直接写出相对应的m的取值范围.

(1)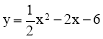 ,(2,﹣8);(2)3<m<8;(3)存在,①当3<m<
,(2,﹣8);(2)3<m<8;(3)存在,①当3<m<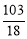 时,存在两个Q点,可作出两个等腰三角形,②当m=
时,存在两个Q点,可作出两个等腰三角形,②当m=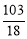 时,存在一个点Q,可作出一个等腰三角形,③当
时,存在一个点Q,可作出一个等腰三角形,③当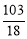 <m<8时,Q点不存在,不能作出等腰三角形.
<m<8时,Q点不存在,不能作出等腰三角形.
【解析】
试题分析:(1)根据已知点的坐标代入已知的函数的解析式即可利用待定系数法确定二次函数的解析式;
(2)首先根据平移确定平移后的函数的解析式,然后确定点P的坐标,然后求得点C的坐标,从而利用待定系数法确定直线AC的解析式,然后确定m的取值范围即可.
(3)∵A(0,﹣6),B(﹣2,0),
∴线段AB的中点坐标为(﹣1,﹣3),直线AB的解析式为y=﹣3x﹣6.
∴过AB的中点且与AB垂直的直线的解析式为: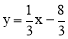 .
.
联立 ,消去y,得
,消去y,得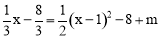 ,即
,即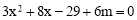 .
.
由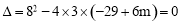 解得.
解得.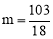
∴①当3<m<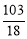 时,存在两个Q点,可作出两个等腰三角形;
时,存在两个Q点,可作出两个等腰三角形;
②当m=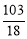 时,存在一个点Q,可作出一个等腰三角形;
时,存在一个点Q,可作出一个等腰三角形;
③当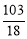 <m<8时,Q点不存在,不能作出等腰三角形.
<m<8时,Q点不存在,不能作出等腰三角形.
试题解析:【解析】
(1)∵A(0,﹣6),B(﹣2,0)在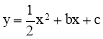 上,
上,
∴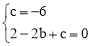 ,解得:
,解得: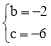 .
.
∴此抛物线的函数关系式为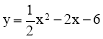 .
.
∵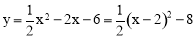 ,∴顶点坐标为(2,﹣8).
,∴顶点坐标为(2,﹣8).
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线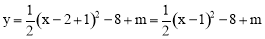 ,
,
∴P(1,﹣8+m),
在抛物线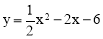 中易得C(6,0),∴直线AC为y2=x﹣6.
中易得C(6,0),∴直线AC为y2=x﹣6.
当x=1时,y2=﹣5,∴﹣5<﹣8+m<0,解得:3<m<8.
(3)存在.
①当3<m<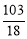 时,存在两个Q点,可作出两个等腰三角形;
时,存在两个Q点,可作出两个等腰三角形;
②当m=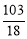 时,存在一个点Q,可作出一个等腰三角形;
时,存在一个点Q,可作出一个等腰三角形;
③当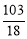 <m<8时,Q点不存在,不能作出等腰三角形.
<m<8时,Q点不存在,不能作出等腰三角形.
考点:1.二次函数综合题;2.线动平移和等腰三角形存在性问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.一元二次方程根的判别式;7.解一元一次不等式组;8.分类思想的应用.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源:2014年初中毕业升学考试(辽宁阜新卷)数学(解析版) 题型:解答题
“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣

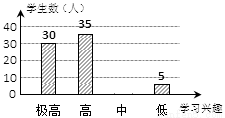
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:选择题
若一粒米的质量约是0.000012kg,将数据0.000012用科学记数法表示为( )
A.12×10-4 B.1.2×10-6 C.1.2×10-5 D.1.2×10-4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州黔西卷)数学(解析版) 题型:选择题
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
如图,为了知道空中一静止的广告气球A的高度,小宇在B处测得气球A的仰角为18°,他向前走了20m到达C处后,再次测得气球A的仰角为45°,已知小宇的眼睛距地面1.6m,求此时气球A距地面的高度(结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:填空题
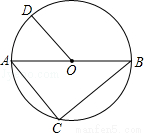
如图,AB是⊙O的直径,点D在⊙O上,∠BOD=130°,AC∥OD交⊙O于点C,连接BC,则∠B= 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com