
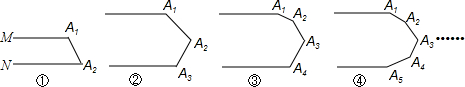
分析 (1)过点A1、…,An分别作MA1的平行线,根据两直线平行,同旁内角互补进行求解;
(2)作A2H∥A1M,根据平行线的性质得到MA1∥NA3,则HA2∥NA3,所以∠1+∠2=180°,∠3+∠4=180°,于是∠A1+∠A2+∠A3=360°.
解答 解:(1)图①中的∠A1+∠A2=180度,
图②中的∠A1+∠A2+∠A3=360度,
图③中的∠A1+∠A2+∠A3+∠A4=540度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720度,
…
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=1800度,
(2)猜想:第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180n度.
(3)图②结论:∠A1+∠A2+∠A3=360度的证明过程如下: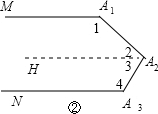
作A2H∥A1M,
∵MA1∥NA3,
∴HA2∥NA3,
∴∠1+∠2=180°,∠3+∠4=180°,
∴∠A1+∠A2+∠A3=∠1+∠2+∠3+∠4=360°.
故答案为180;360;540;720;1800;180n;360°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 24029 | B. | 3×22014 | C. | -22014 | D. | ($\frac{1}{2}$)2014 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50).
如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是菱形,过点A、C作对角线AC的垂线,分别交CD和AB的延长线于点E、F.已知AE=2,四边形AECF的周长为12,则菱形的边长为( )
如图,四边形ABCD是菱形,过点A、C作对角线AC的垂线,分别交CD和AB的延长线于点E、F.已知AE=2,四边形AECF的周长为12,则菱形的边长为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
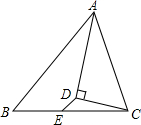 已知△ABC中,AB=6,AC=5,从点C向∠A的平分线作垂线,垂足为D,E为BC中点,则DE的长是( )
已知△ABC中,AB=6,AC=5,从点C向∠A的平分线作垂线,垂足为D,E为BC中点,则DE的长是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com