
【题目】如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=﹣ ![]() x2﹣2x+c经过点A、B,抛物线的顶点为C.
x2﹣2x+c经过点A、B,抛物线的顶点为C.
(1)∠BAO=°;
(2)求tan∠CAB的值;
(3)在抛物线上是否存在点P,能够使∠PCA=∠BAC?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】
(1)45
(2)
解:由(1)得:B(0,n),A(﹣n,0),
∵抛物线y=﹣ ![]() x2﹣2x+c经过点A、B
x2﹣2x+c经过点A、B
∴  ,解得
,解得 ![]() 或
或 ![]() (舍去)
(舍去)
∴A(﹣6,0),B(0,6),直线AB的解析式为:y=x+6,
抛物线为:y=﹣ ![]() ﹣2x+6=﹣
﹣2x+6=﹣ ![]() (x+2)2+8,
(x+2)2+8,
∴抛物线的顶点为C(﹣2,8),
设抛物线的对称轴为直线l,连结BC,
如图1,过点B作BD⊥l,则BD=CD=2,BD∥x轴,
∴∠CBD=45°,
又BD∥x轴,
∴∠DBA=∠BAO=45°,
∴∠CBA=∠CBD+∠DBA=90°,
在Rt△CDB中,BC= ![]() =2
=2 ![]() ,
,
在Rt△AOB中,AB= ![]() =6
=6 ![]() ,
,
∴在Rt△ABC中,tan∠CAB= ![]() =
= ![]()

(3)
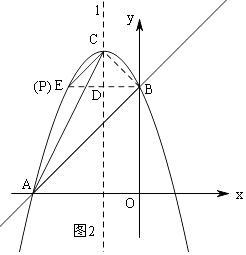
解:①当点P在CA左侧时,如图2,
延长BD交抛物线于点E,当∠PCA=∠BAC时,CP∥AB,
此时,点P与点E重合,点P的坐标是(﹣4,6);
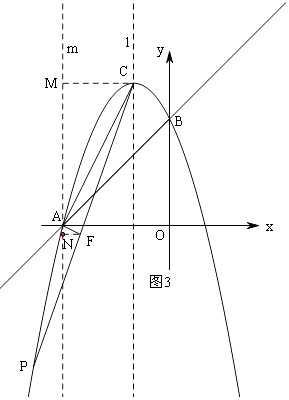
②当点P在CA右侧时,如图3,过点A作AC的垂线交CP于点F,
过点A作y轴的平行线m,过点C作CM⊥m,过点F作FN⊥m,
由于tan∠BAC= ![]() ,所以tan∠ACF=tan∠ACP=
,所以tan∠ACF=tan∠ACP= ![]() ,
,
∵Rt△CMA∽Rt△ANF,
∴ ![]() ,
, ![]() ,AN=
,AN= ![]() CM=
CM= ![]() ,NF=
,NF= ![]() MA=
MA= ![]() ,
,
∴F(﹣ ![]() ,﹣
,﹣ ![]() );
);
易求得直线CF的解析式为:y=7x+22,
由 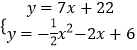 ,消去y,得x2+18x+32=0,
,消去y,得x2+18x+32=0,
解得x=16或x=﹣2(舍去),
因此点P的坐标(﹣16,﹣90);
综上所述,P的坐标是(﹣4,6)或(﹣16,﹣90).
【解析】解:(1)y=x+n,
当x=0时,y=n,则B(0,n),
当y=0时,x=﹣n,则A(﹣n,0),
∴OA=OB=n,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
所以答案是:45;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
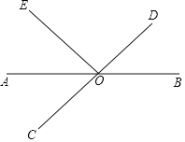
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=80°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图. 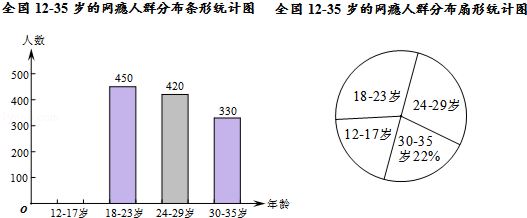
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,BC=12. 
(1)用尺规作图的方法作AB的垂直平分线MN,分别交BC、AB于点M、N(保留作图痕迹,不要求写作法);
(2)求第(1)题中的CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.
(1)填空:OHOF (“>”、“<”、“=”);
(2)当四边形EFGH为矩形时,请问线段AE与AH应满足什么数量关系;
(3)当四边形EFGH为正方形时,AO与EH交于点P,求OP2+PHPE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com