
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 ![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) 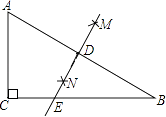
A.2
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:在Rt△ACB中,由勾股定理得:BC= ![]() =4,
=4,
连接AE,
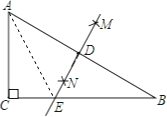
从作法可知:DE是AB的垂直平分线,
根据性质得出AE=BE,
在Rt△ACE中,由勾股定理得:AC2+CE2=AE2,
即32+(4﹣AE)2=AE2,
解得:AE= ![]() ,
,
在Rt△ADE中,AD= ![]() AB=
AB= ![]() ,由勾股定理得:DE2+(
,由勾股定理得:DE2+( ![]() )2=(
)2=( ![]() )2,
)2,
解得:DE= ![]() .
.
故选C.
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
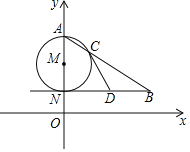
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H. 
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG= ![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示: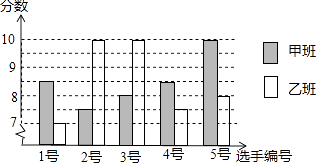
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程,并解答后面的问题:
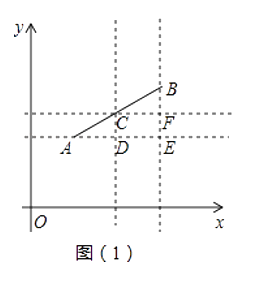
如图1,在平面直角坐标系xOy中,A(x1 , y1),B(x2 , y2),C为线段AB的中点,求C点的坐标.
解:分布过A、C做x轴的平行线,过B、C做y轴的平行线,两组平行线的交点如图1所示.
设C(x0 , y0),则D(x0 , y1),E(x2 , y1),F(x2 , y0)
由图1可知:x0= ![]() =
= ![]()
y0= ![]() =
= ![]()
∴( ![]() ,
, ![]() )
)
问题:
(1)已知A(﹣1,4),B(3,﹣2),则线段AB的中点坐标为
(2)平行四边形ABCD中,点A、B、C的坐标分别为(1,﹣4),(0,2),(5,6),求点D的坐标.
(3)如图2,B(6,4)在函数y= ![]() x+1的图象上,A(5,2),C在x轴上,D在函数y=
x+1的图象上,A(5,2),C在x轴上,D在函数y= ![]() x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.
x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.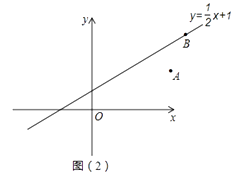
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,AB=1,则EF的长是( ) 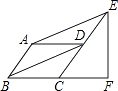
A.1.5
B.![]()
C.![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com