
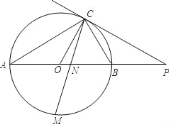
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
【答案】(1)见解析;
(2)见解析;
(3)MNMC=8.
【解析】
试题分析:(1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;
(2)AB是直径;故只需证明BC与半径相等即可;
(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC;代入数据可得MNMC=BM2=8.
试题解析:(1)∵OA=OC,∴∠A=∠ACO.又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.又∵AB是⊙O的直径,∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.即OC⊥CP,∵OC是⊙O的半径.∴PC是⊙O的切线.
(2)∵AC=PC,∴∠A=∠P,∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,∴BC=OC.∴BC=![]() AB.
AB.
(3)连接MA,MB,∵点M是![]() 的中点,∴
的中点,∴![]() ,∴∠ACM=∠BCM.
,∴∠ACM=∠BCM.
∵∠ACM=∠ABM,∴∠BCM=∠ABM.∵∠BMN=∠BMC,∴△MBN∽△MCB.
∴![]() .∴BM2=MNMC.又∵AB是⊙O的直径,
.∴BM2=MNMC.又∵AB是⊙O的直径,![]() ,
,
∴∠AMB=90°,AM=BM.∵AB=4,∴BM=2![]() .
.
∴MNMC=BM2=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某服装厂有工人54人,每人每天可加工上衣8件或裤子10条,应怎样分配人数,才能使每天生产的上衣和裤子配套?设x人做上衣,则做裤子的人数为________人,根据题意,可列方程为_______,解得x=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元代朱世杰所著的《算学启蒙》里有这样一道题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”请你回答:良马_______天可以追上驽马.
查看答案和解析>>
科目:初中数学 来源: 题型:
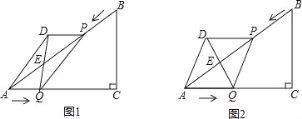
【题目】如图1,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)用含有t的代数式表示AE= .
(2)当t为何值时,平行四边形AQPD为矩形.
(3)如图2,当t为何值时,平行四边形AQPD为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com