
【题目】小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).

(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
【答案】(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看出12:00时他到达离家最远的地方,离家30千米. (4)由图象看出11时距家19千米,12时距家30千米,11时到12时他行驶了30- 19=11(千米). (5)由图象看出12:00~13:00时距离没变且时间较长,得12:00~13:00休息并吃午餐. (6)由图象看出回家时用了2小时,路程是30千米,所以回家的平均速度是30÷2=15(千米/时).


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国2013年到2017年国内生产总值情况.(以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》,其中国内生产总值绝对数按现价计算,增长速度按不变价格计算)

根据统计图提供的信息,下列推断合理的是
A.从2013-2017年,我国国内生产总值逐年下降
B.从2013-2017年,我国国内生产总值的增长率逐年下降
C.从2013-2017年,我国国内生产总值的平均增长率约为6.7%
D.计算同上年相比的增量,2017年我国国内生产总值的增量为近几年最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是( )
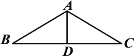
A.AB和AD,点AB.AB和AC,点B
C.AC和BC, 点CD.AD和BC,点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y = x2 - 4x + 3.
(1)用配方法将y = x2 - 4x + 3化成y = a(x - h)2 + k的形式;
(2)在平面直角坐标系![]() 中画出该函数的图象;
中画出该函数的图象;
(3)当0≤x≤3时,y的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为______元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为“特征多项式”,例如第1格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为____________,
第4格的“特征多项式”为____________,
第![]() 格的“特征多项式”为____________;
格的“特征多项式”为____________;
(2)若第1格的“特征多项式”的值为10,第2格的“特征多项式”的值为19,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com