练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】拖拉机开始工作时，油箱中有油30L，每小时耗油5L．

    （1）写出油箱中的剩余测量Q（L）与工作时间t（h）之间的函数表达式，并求出自变量t的取值范围；

    （2）当拖拉机工作4h时，油箱内还剩余油多少升？

    【答案】（1）Q＝30﹣5t（0≤t≤6）；（2）10L

    【解析】

    （1）根据“油箱中的余油量=油箱中原有油量-消耗的油量”，即可列出函数解析式和自变量的取值范围；

    （2）把t＝4代入函数解析式，即可得到答案．

    （1）由题意可得，油箱中的余油量Q（L）与工作时间t（h）之间的函数关系是：Q＝30﹣5t（0≤t≤6）；

    （2）把t＝4代入，得Q＝30﹣5t＝30-5×4＝10，

    答：当拖拉机工作4h时，油箱内还剩余油10L．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

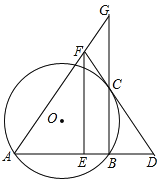
    【题目】如图，AB是⊙O的弦，过B作BC⊥AB交⊙O于点C，过C作⊙O的切线交AB的延长线于点D，取AD的中点E,过E作EF∥BC交DC 的延长线与点F，连接AF并延长交BC的延长线于点G．

    求证：（1）FC=FG （2）=BCCG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中将点A（3，2）向y轴的负方向平移3个单位长度所得点的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对单项式“5x”，我们可以这样来解释：某人以5千米/小时的速度走了x小时，他一共走的路程是5x千米，请你对“5x”再给出另一个生活实际方面的解释_________________________________元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2017年北京市在经济发展、社会进步、城市建设、民生改善等方面取得新成绩、新面貌．综合实力稳步提升．全市地区生产总值达到280000亿元，将280000用科学记数法表示为（　　）

    A. 280×103B. 28×104C. 2.8×105D. 0.28×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是一个用铁丝围成的篮框，我们来仿制一个类似的柱体形篮框．如图2，它是由一个半径为r、圆心角90°的扇形A2OB2，矩形A2C2EO、B2D2EO，及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn，OEFG围成，其中A1、G、B1在上，A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上，C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上，EF⊥C2D2于H2，C1D1⊥EF于H1，FH1=H1H2=d，C1D1、C2D2、C3D3、CnDn依次等距离平行排放（最后一个矩形状框的边CnDn与点E间的距离应不超过d），A1C1∥A2C2∥A3C3∥…∥AnCn．

    （1）求d的值；

    （2）问：CnDn与点E间的距离能否等于d？如果能，求出这样的n的值，如果不能，那么它们之间的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个长方形的周长是30厘米，若长方形的一边用字母x（厘米）表示，则该长方形的面积是（　　）
    A.x（30﹣2x）平方厘米
    B.x（30﹣x）平方厘米
    C.x（15﹣x）平方厘米
    D.x（15+x）平方厘米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景：

    如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．

    小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=CD，从而得出结论：AC+BC=CD．

    简单应用：

    （1）在图①中，若AC=，BC=，则CD= ．

    （2）如图③，AB是⊙O的直径，点C、D在⊙上，，若AB=13，BC=12，求CD的长．

    拓展规律：

    （3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）

    （4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE=AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】江苏是全国首个自然村“村村通宽带”省份．我市某村为了将当地农产品外销，建立了淘宝网店．该网店于今年7月底以每袋25元的成本价收购一批农产品．当商品售价为每袋40元时，8月份销售256袋．9、10月该商品十分畅销．销售量持续走高．在售价不变的基础上，10月份的销售量达到400袋．设9、10这两个月月平均增长率不变．

    （1）求9、10这两个月的月平均增长率；

    （2）为迎接双“十一”，11月份起，该网店采用降价促销的方式回馈顾客，经调查发现，该农产品每降价1元/每袋，销售量就增加5袋，当农产品每袋降价多少元时，该淘宝网店11月份获利4250元？

    查看答案和解析>>

    同步练习册答案