
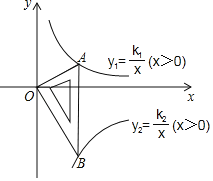
【题目】如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=![]() 图象上,顶点B在函数y2=
图象上,顶点B在函数y2=![]() 的图象上,则
的图象上,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α等于( )
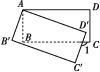
A. 20° B. 30° C. 40° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算2个小球上的数字之和.记录后将小球放回袋中搅匀,进行重复试验,试验数据如下表:
摸球总 次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果试验继续进行下去,根据上表提供的数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是________;
(2)如果摸出的2个小球上数字之和为9的概率是,那么x的值可以为7吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,深圳高级中学(集团)南北校区初三学生参加东校区下午![]() 时的交流活动,南校区学生中午
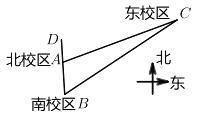
时的交流活动,南校区学生中午![]() 乘坐校车出发,沿正北方向行12公里到达北校区,然后南北校区一同前往东校区(等待时间不计).如图所示,已知东校区在南校区北偏东
乘坐校车出发,沿正北方向行12公里到达北校区,然后南北校区一同前往东校区(等待时间不计).如图所示,已知东校区在南校区北偏东![]() 方向,在北校区北偏东
方向,在北校区北偏东![]() 方向.校车行驶状态的平均速度为
方向.校车行驶状态的平均速度为![]() ,途中一共经过30个红绿灯,平均每个红绿灯等待时间为30秒.
,途中一共经过30个红绿灯,平均每个红绿灯等待时间为30秒.
(1)求北校区到东校区![]() 的距离;
的距离;
(2)通过计算,说明南北校区学生能否在![]() 前到达东校区.(本题参考数据:
前到达东校区.(本题参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
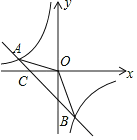
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有东西方向的街道3条,南北方向的街道4条,从位置A出发沿街道行走到达位置B,要求路程最短,研究有多少种不同的走法. 小聪是这样思考的:要使路程最短,就不能走“回头路”,只能分五步来完成,其中三步向右行进,两步向上行进,如果用数字“1”表示向右行走一格,数字“2”表示向上行走一格,如“11221”与“11212”就表示两种符合要求的不同走法,那么符合要求的不同走法的种数为( )
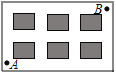
A. 6种B. 8种C. 10种D. 12种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:不在同一直线上的三点A,B,C
求作:⊙O,使它经过点A,B,C
作法:如图,
(1)连接AB ,作线段AB的垂直平分线DE;
(2)连接BC ,作线段BC的垂直平分线FG,交DE于点O;
(3)以O为圆心,OB 长为半径作⊙O.
⊙O就是所求作的圆.
根据以上作图过程及所作图形,下列结论中正确的是( )
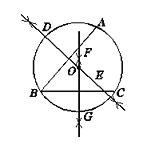
A.连接AC, 则点O是△ABC的内心B.![]()
C.连接OA,OC,则OA, OC不是⊙![]() 的半径D.若连接AC, 则点O在线段AC的垂直平分线上
的半径D.若连接AC, 则点O在线段AC的垂直平分线上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com