
【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
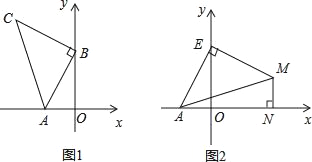
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
【答案】(1)C(-4,6);(2)存在,(-6,2)或(2,-2)或(4,2)或(-4,6);(3)2.
【解析】
试题(1)作CE⊥y轴于E,证明△CBE≌△BAO即可得出结论;(2)分为四种情况讨论:①当P和C重合时,△PAB和△ABC全等,即此时P的坐标是(-4,6);②点P在第二象限,过P作PE⊥x轴于E,满足∠PAB=∠AOB=∠PEA=90°,PA=AB,则此时△PAB和△ABC全等,证明△PEA≌△AOB即可得出P点坐标;③点P在第一象限,作∠CAP=90°,交CB的延长线于P,此时△PAB和△ABC全等,过P作PE⊥x轴于E,证明△CMA≌△AEP即可求得P点坐标;④P点在第四象限,作∠BAP=90度,AP=AB,此时△PAB和△ABC全等,证明△AOB≌△PEA即可求出P点坐标;(3)作MF⊥y轴于F,把OE-MN转化成OE-OF,于是OE-MN就等于EF的值,然后证明△AEO≌△EMF,把EF值转化成AO的长度,就求出了OE-MN的结果.
试题解析:(1)作CE⊥y轴于E,如图1,
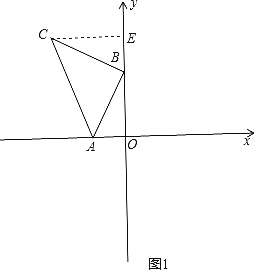
∵A(-2,0),B(0,4),∴OA=2,OB=4,∵∠CBA=90°,∴∠CEB=∠AOB=∠CBA=90°,∴∠ECB+∠EBC=90°∠CBE+∠ABO=90°,∴∠ECB=∠ABO,在△CBE和△BAO中,∠ECB=∠ABO,∠CEB=∠AOB,BC=AB,∴△CBE≌△BAO(AAS),∴CE=BO=4,BE=AO=2,即OE=2+4=6,因为C点在第二象限,∴C(-4,6).
(2)分四种情况讨论:①如图2,当P和C重合时,△PAB和△ABC全等,即此时P的坐标是(-4,6);
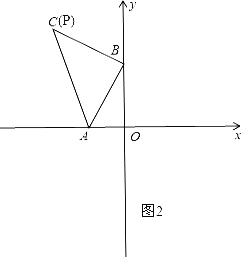
②如图3,点P在第二象限,过P作PE⊥x轴于E,满足∠PAB=∠AOB=∠PEA=90°,PA=AB,则此时△PAB和△ABC全等,∵∠EPA+∠PAE=90°,∠PAE+∠BAO=90°,∴∠EPA=∠BAO(同角的余角相等),在△PEA和△AOB中,∠EPA=∠BAO,∠PEA=∠AOB,PA=AB,∴△PEA≌△AOB,∴PE=AO=2,EA=BO=4,∴OE=2+4=6,即P的坐标是(-6,2);
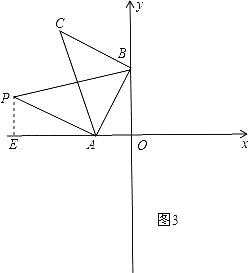
③如图4,点P在第一象限,作∠CAP=90°,交CB的延长线于P,此时△PAB和△ABC全等,过P作PE⊥x轴于E,过C作CM⊥x轴于M,
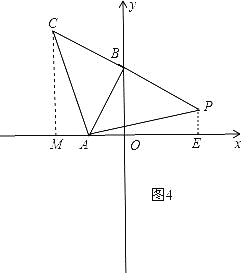
则∠CMA=∠PEA=90°,∵△CBA≌△PBA,∴∠PAB=∠CAB=45°,AC=AP,∴∠CAP=90°,∴∠MCA+∠CAM=90°,∠CAM+∠PAE=90°,∴∠MCA=∠PAE,在△CMA和△AEP中,∠MCA=∠PAE,∠CMA=∠PEA,AC=AP,∴△CMA≌△AEP,∴PE=AM,CM=AE,∵C(-4,6),A(-2,0),
∴PE=AM=4-2=2,OE=AE-A0=6-2=4,即P的坐标是(4,2);
④如图5,P点在第四象限,作∠BAP=90度,AP=AB,此时△PAB和△ABC全等,过P作PE⊥x轴于E,
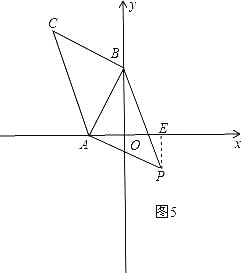
∵△CBA≌△PAB,∴AB=AP,∠CBA=∠BAP=90°,则∠AEP=∠AOB=90°,∴∠BAO+∠PAE=90°,∠PAE+∠APE=90°,∴∠BAO=∠APE,在△AOB和△PEA中,∠BAO=∠APE,∠AOB=∠PEA,AB=AP,∴△AOB≌△PEA,∴PE=AO=2,AE=OB=4,∴0E=AE-AO=4-2=2,即P的坐标是(2,-2).综上所述:坐标平面内存在一点P,使△PAB与△ABC全等,符合条件的P的坐标是(-6,2)或(2,-2)或(4,2)或(-4,6).(3)如图6,作MF⊥y轴于F,
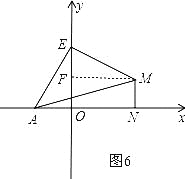
则∠AEM=∠EFM=∠AOE=90°,∵∠AEO+∠MEF=90°,∠MEF+∠EMF=90°,∴∠AEO=∠EMF,在△AOE和△EMF中,∠AOE=∠EFM,∠AEO=∠EMF,AE=EM,∴△AEO≌△EMF,∴EF=AO=2,MF=OE,∵MN⊥x轴,MF⊥y轴,∴∠MFO=∠FON=∠MNO=90°,∴四边形FONM是矩形,∴MN=OF,∴OE-MN=OE-OF=EF=OA=2.即OE-MN的值是2.


科目:初中数学 来源: 题型:
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:图象①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1P2P3,第二次移动后图形①②③的圆心依次为P4P5P6…,依此规律,P0P2018=_____个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
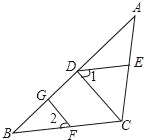
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:p为实数.
p | k | q |
… | … | … |
3 | 16×3+26 | 2×2×6 |
4 | 16×4+26 | 2×3×7 |
5 | 16×5+26 | 2×4×8 |
6 | 16×6+26 | 2×5×9 |
7 | 16×7+26 | 2×6×10 |
… | … | … |
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38?
(2)当p为何值时,k与q的值相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活与数学
(1)莹莹在日历上圈出三个数,呈大写的“一”字,这三个数的和是中间数的 倍,莹莹又在日历上圈出5个数,呈“十”字框形,它们的和是50,则中间的数是 :
(2)小丽同学也在某月的日历上圈出如图所示“七”字形,发现这八个数的和是125,那么这八个数中最大数为 :
(3)在第(2)题中这八个数之和 为101(填“能”或“不能”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com