
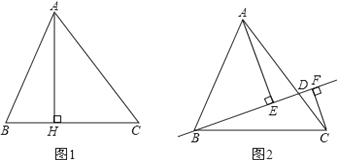
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
【答案】探究:12,15,84;拓展:(1)![]() ,
,![]() ;(2)
;(2)![]() ;x=
;x=![]() 时,(
时,(![]() )的最大值为15;当
)的最大值为15;当![]() 时,(
时,(![]() )的最小值为12;(3)
)的最小值为12;(3)![]() 或
或![]() ;发现:
;发现:![]() .
.
【解析】
探究:由![]() ,AB=13,可得BH的长,即可求出CH的长,利用勾股定理求出AH、AC的长即可;拓展:(1)由三角形的面积公式即可求解;(2)首先由(1)可得
,AB=13,可得BH的长,即可求出CH的长,利用勾股定理求出AH、AC的长即可;拓展:(1)由三角形的面积公式即可求解;(2)首先由(1)可得![]() ,
,![]() ,再根据S△ABD+S△CBD=S△ABC=84,即可求出(m+n)与x的函数关系式,然后由点D在AC上(可与点A,C重合),可知x的最小值为AC边上的高,最大值为BC的长;根据反比例函数的性质即可得答案;(3)由于BC>BA,所以当以B为圆心,以大于
,再根据S△ABD+S△CBD=S△ABC=84,即可求出(m+n)与x的函数关系式,然后由点D在AC上(可与点A,C重合),可知x的最小值为AC边上的高,最大值为BC的长;根据反比例函数的性质即可得答案;(3)由于BC>BA,所以当以B为圆心,以大于![]() 且小于13为半径画圆时,与AC有两个交点,不符合题意,故根据点D的唯一性,分两种情况:①当BD为△ABC的边AC上的高时,D点符合题意;②当AB<BD≤BC时,D点符合题意;发现:由于AC>BC>AB,所以使得A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线.
且小于13为半径画圆时,与AC有两个交点,不符合题意,故根据点D的唯一性,分两种情况:①当BD为△ABC的边AC上的高时,D点符合题意;②当AB<BD≤BC时,D点符合题意;发现:由于AC>BC>AB,所以使得A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线.
探究:∵![]() ,AB=13,
,AB=13,
∴BH=5,
∴![]() ,
,
∴HC=9,![]() ,
,
∴S△ABC=![]() ×12×14=84,
×12×14=84,
故答案为12,15,84;
拓展:解:(1)由三角形面积公式得出:![]() ,
,![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵AC边上的高为:![]() ,
,
∴x的取值范围为:![]() ,
,
∵(![]() )随
)随![]() 的增大而减小,
的增大而减小,
∴![]() 时,(
时,(![]() )的最大值为:15;
)的最大值为:15;
当![]() 时,(
时,(![]() )的最小值为12;
)的最小值为12;
(3)∵BC>BA,只能确定唯一的点D,
∴当以B为圆心,以大于![]() 且小于13为半径画圆时,与AC有两个交点,不符合题意,
且小于13为半径画圆时,与AC有两个交点,不符合题意,
①当BD为△ABC的边AC上的高时,即x=![]() 时,BD与AC有一个交点,符合题意,
时,BD与AC有一个交点,符合题意,
②当AB<BD≤BC时,即![]() 时,BD与AC有一个交点,符合题意,
时,BD与AC有一个交点,符合题意,
∴x的取值范围是![]() 或
或![]() ,
,
发现:
∵AC>BC>AB,
∴AC、BC、AB三边上的高中,AC边上的高最短,
∴过A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线,最小值为AC边上的高的长![]() .
.


科目:初中数学 来源: 题型:
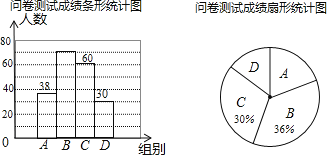
【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
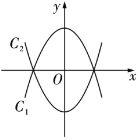
【题目】如图,已知拋物线![]() ,将抛物线
,将抛物线![]() 沿
沿![]() 轴翻折,得到拋物线
轴翻折,得到拋物线![]() .
.
(1)求出抛物线![]() 的函数表达式;
的函数表达式;
(2)现将抛物线![]() 向左平移
向左平移![]() 个单位长度,平移后得到的新抛物线的顶点为
个单位长度,平移后得到的新抛物线的顶点为![]() ,与
,与![]() 轴的交点从左到右依次为
轴的交点从左到右依次为![]() ,
,![]() ;将抛物线
;将抛物线![]() 向右也平移
向右也平移![]() 个单位长度,平移后得到的新抛物线的顶点为
个单位长度,平移后得到的新抛物线的顶点为![]() ,与
,与![]() 轴交点从左到右依次为
轴交点从左到右依次为![]() ,
,![]() .在平移过程中,是否存在以点
.在平移过程中,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是矩形的情形?若存在,请求出此时
为顶点的四边形是矩形的情形?若存在,请求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
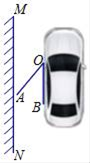
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=_____°.
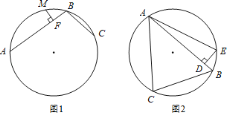
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,若CD=5,以D为圆心,DC长为半径作⊙D交CA的延长线于E,过D作DF⊥AC,垂足为F,且DF=3.
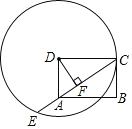
(1)求证:BC是⊙D的切线;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级学生步行到郊外春游.一班的学生组成前队,速度为4km/h ,二班的学生组成后队,速度为6km/h .前队出发1h 后,后队才出发,同时,后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.若不计队伍的长度,如图,折线ABC ,A-B-C 分别表示后队,联络员在行进过程中,离前队的路程 与后队行进时间x(h) 之间的部分函数图象.
(1) 求线段AB 对应的函数关系式;
(2) 求点E 的坐标,并说明它的实际意义;
(3) 联络员从出发到他折返后第一次与后队相遇的过程中,当x 为何值时,他离前队的路程与他离后队的路程相等?
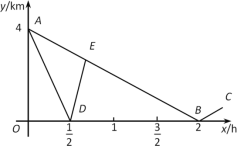
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成任务.
三角形的外心
定义:三角形三边的垂直平分线相交于一点,这个点叫做三角形的外心.
如图1,直线l1,l2,l3分别是边AB,BC,AC的垂直平分线.
求证:直线l1,l2,l3相交于一点.
证明:如图2,设l1,l2相交于点O,分别连接OA,OB,OC
∵l1是AB的垂直平分线,
∴OA=OB,(依据1)
∵l2是BC的垂直平分线,
∴OB=OC,
∴OA=OC,(依据2)
∵l3是AC的垂直平分线,
∴点O在l3上,(依据3)
∴直线l1,l2,l3相交于一点.
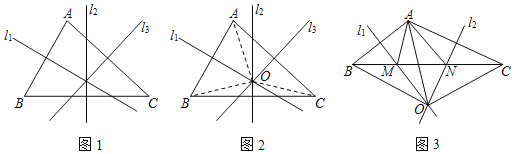
(1)上述证明过程中的“依据1”“依据2”“依据3”分别指什么?
(2)如图3,直线l1,l2分别是AB,AC的垂直平分线,直线l1,l2相交于点O,点O是△ABC的外心,l1交BC于点N,l2交BC于点N,分别连接AM、AN、OA、OB、OC.若OA=6cm,△OBC的周长为22cm,求△AMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com