
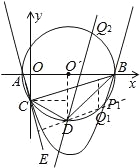
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3.(2)y=x﹣9.(3)存在,P1(
x﹣3.(2)y=x﹣9.(3)存在,P1(![]() ,
,![]() ),P2(14,25).
),P2(14,25).
【解析】
试题分析:(1)已知了A、B两点的坐标即可得出OA、OB的长,在直角三角形ACB中由于OC⊥AB,因此可用射影定理求出OC的长,即可得出C点的坐标.然后用待定系数法即可求出抛物线的解析式;(2)本题的关键是得出D点的坐标,CD平分∠BCE,如果连接O′D,那么根据圆周角定理即可得出∠DO′B=2∠BCD=∠BCE=90°,由此可得出D的坐标为(4,﹣5).根据B、D两点的坐标即可用待定系数法求出直线BD的解析式;(3)本题要分两种情况进行讨论:①过D作DP∥BC,交D点右侧的抛物线于P,此时∠PDB=∠CBD,可先用待定系数法求出直线BC的解析式,然后根据BC与DP平行,那么直线DP的斜率与直线BC的斜率相同,因此可根据D的坐标求出DP的解析式,然后联立直线DP的解析式和抛物线的解析式即可求出交点坐标,然后将不合题意的舍去,即可得出符合条件的P点.②同①的思路类似,先作与∠CBD相等的角:在O′B上取一点N,使BN=BM.可通过证△NBD≌△MDB,得出∠NDB=∠CBD,然后同①的方法一样,先求直线DN的解析式,进而可求出其与抛物线的交点即P点的坐标.综上所述可求出符合条件的P点的值.
试题解析:(1)∵以AB为直径作⊙O′,交y轴的负半轴于点C,∴∠OCA+∠OCB=90°,又∵∠OCB+∠OBC=90°,∴∠OCA=∠OBC,又∵∠AOC=∠COB=90°,∴△AOC∽△COB,∴![]() .又∵A(﹣1,0),B(9,0),∴
.又∵A(﹣1,0),B(9,0),∴![]() ,解得OC=3(负值舍去).∴C(0,﹣3),故设抛物线解析式为y=a(x+1)(x﹣9),∴﹣3=a(0+1)(0﹣9),解得a=
,解得OC=3(负值舍去).∴C(0,﹣3),故设抛物线解析式为y=a(x+1)(x﹣9),∴﹣3=a(0+1)(0﹣9),解得a=![]() ,∴二次函数的解析式为y=
,∴二次函数的解析式为y=![]() (x+1)(x﹣9),即y=
(x+1)(x﹣9),即y=![]() x2﹣
x2﹣![]() x﹣3.(2)∵AB为O′的直径,且A(﹣1,0),B(9,0),∴OO′=4,O′(4,0),∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,∴∠BCD=
x﹣3.(2)∵AB为O′的直径,且A(﹣1,0),B(9,0),∴OO′=4,O′(4,0),∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,∴∠BCD=![]() ∠BCE=
∠BCE=![]() ×90°=45°,连接O′D交BC于点M,则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=
×90°=45°,连接O′D交BC于点M,则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=![]() AB=5.∴O′D⊥x轴,∴D(4,﹣5).∴设直线BD的解析式为y=kx+b,∴
AB=5.∴O′D⊥x轴,∴D(4,﹣5).∴设直线BD的解析式为y=kx+b,∴![]() ,解得
,解得![]() ,∴直线BD的解析式为y=x﹣9.(3)∵C(0,﹣3),设在抛物线上存在点P,使得∠PDB=∠CBD,设射线DP交⊙O′于点Q,则 弧BQ=弧CD.分两种情况(如图所示):①∵O′(4,0),D(4,﹣5),B(9,0),C(0,﹣3).∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,因此,点Q1(7,﹣4)符合 弧BQ=弧CD,∵D(4,﹣5),Q1(7,﹣4),∴用待定系数法可求出直线DQ1解析式为y=
,∴直线BD的解析式为y=x﹣9.(3)∵C(0,﹣3),设在抛物线上存在点P,使得∠PDB=∠CBD,设射线DP交⊙O′于点Q,则 弧BQ=弧CD.分两种情况(如图所示):①∵O′(4,0),D(4,﹣5),B(9,0),C(0,﹣3).∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,因此,点Q1(7,﹣4)符合 弧BQ=弧CD,∵D(4,﹣5),Q1(7,﹣4),∴用待定系数法可求出直线DQ1解析式为y=![]() x﹣
x﹣![]() .解方程组
.解方程组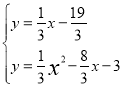 ,得
,得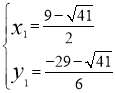 或
或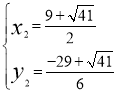 ,∴点P1坐标为(
,∴点P1坐标为(![]() ,
,![]() ),坐标为(
),坐标为(![]() ,
,![]() )不符合题意,舍去.②∵Q1(7,﹣4),∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合 弧BQ=弧CD,∵D(4,﹣5),Q2(7,4).∴用待定系数法可求出直线DQ2解析式为y=3x﹣17.解方程组
)不符合题意,舍去.②∵Q1(7,﹣4),∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合 弧BQ=弧CD,∵D(4,﹣5),Q2(7,4).∴用待定系数法可求出直线DQ2解析式为y=3x﹣17.解方程组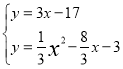 得
得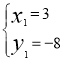 或
或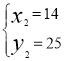 ,∴点P2坐标为(14,25),坐标为(3,﹣8)不符合题意,舍去.∴符合条件的点P有两个:P1(
,∴点P2坐标为(14,25),坐标为(3,﹣8)不符合题意,舍去.∴符合条件的点P有两个:P1(![]() ,
,![]() ),P2(14,25).
),P2(14,25).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分100分)分成四类,并制作了如下的统计图表:
类别 | 甲 | 乙 | 丙 | 丁 |
成绩 | 60≤m<70 | 70≤m<80 | 80≤m<90 | 90≤m<100 |
频数 | 5 | 10 | a | b |
根据图表信息,回答下列问题:
(1)该班共有学生 人,表中a= ,b= ;
(2)扇形图中,丁类所对应的圆心角是 度;
(3)已知A同学在丁类中,现从丁类同学中随机抽两名同学参加学校的决赛,请用列举的方法求A同学能够参加决赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1号探测气球从海拔5 m处出发,以l m/min的速度上升.与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升,两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50).
(1)根据题意,填写下表:
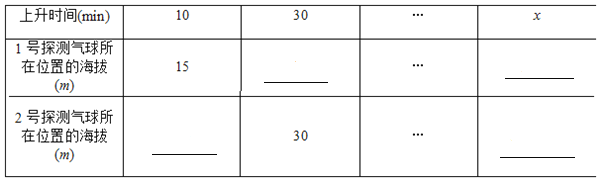
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
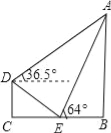
【题目】如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶上D点处测得条幅顶端A的仰角为36.5°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为64°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度为 米.
(结果精确到0.1米,参考数据sin36.5°≈0.6,tan36.5°≈0.75,sin64°≈0.9,tan64°≈2.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com