
【题目】1号探测气球从海拔5 m处出发,以l m/min的速度上升.与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升,两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50).
(1)根据题意,填写下表:
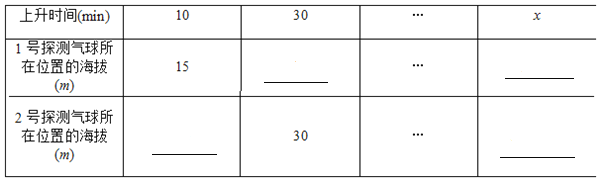
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
【答案】(1)20,35,x+5,0.5x+15;(2)此时气球上升了20 min,都位于海拔25 m的高度.(3)15 m.
【解析】试题分析:(Ⅰ)由题意可得,1号探测气球从海拔5 m处出发,以1m/min的速度上升,30min时1号探测气球的海拔高度为35m,xmin时海拔高度为(x+5)m;2号探测气球从海拔15m处出发,以0.5m/min的速度上升,10min时2号探测气球的海拔高度为20m,xmin时海拔高度为(0.5x+15)m.
(Ⅱ)令x+5=0.5x+15,若x有解且x的值位于0≤x≤50这个范围,则说明在某时刻两个气球能位于同一高度,这时求得x的值再带入求气球的海拔高度即可,若x有解且x的值不位于0≤x≤50这个范围,则不存在某时刻两个气球位于同一高度.
(Ⅲ)当30≤x≤50时,由题意,可知1号气球所在位置的海拔始终高于2号气球,设两个气球在同一时刻所在位置的海拔相差有y米,用x表示出y,根据所得的关系式及x的取值范围,即可求得两个气球所在位置的海拔高度相差的最大值.
试题解析:(Ⅰ)35,x+5;20,0.5x+15.
(Ⅱ)两个气球能位于同一高度.
根据题意,x+5=0.5x+15,解得x=20.
有x+5=25.
答:此时,气球上升了20min,都位于海拔25m的高度.
(Ⅲ))当30≤x≤50时,
由题意,可知1号气球所在位置的海拔始终高于2号气球,
设两个气球在同一时刻所在位置的海拔相差有y米,
则y=(x+5)—(0.5x+15)=0.5x—10.
∵0.5>0,
∴y随x的增大而增大.
∴当x=50时,y取得最大值15.
答:两个气球所在位置的海拔最多相差15米.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 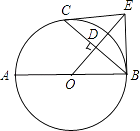
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于20.55与2.055这两个近似数,下列说法中,正确的是( ).
A.它们的有效数字与精确位数都不相同
B.它们的有效数字与精确位数都相同
C.它们的精确位数不相同,有效数字相同
D.它们的有效数字不相同,精确位数相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
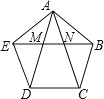
A.EM:AE=2:(![]() -1)
-1)
B.MN:EM=(![]() -1):(3-
-1):(3-![]() )
)
C.AM:MN=(3-![]() ):(
):(![]() -1)
-1)
D.MN:DC=(3-![]() ):2
):2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:﹣14﹣| ![]() ﹣1|×
﹣1|× ![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
(2)先化简,再求值:(5a2﹣3b2)+3(a2﹣2b2)﹣2(5a2﹣2b2),其中a=﹣1,b=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com