
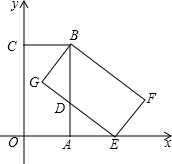
 如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.
如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.分析 (1)连接BO、BE,根据矩形的性质易得BO=BE,BA⊥OE,根据等腰三角形三线合一的性质可得结论;
(2)易证△BGD≌△EAD,得到AD=GD,BD=ED,在△EAD中,设AD=x,根据勾股定理列方程即可;
(3)作FH⊥x轴于点H,易证△DAE∽△EHF,根据对应边成比例列方程求出EH,进而求出OH和FH,可知点F的坐标.
解答 解:(1)如图,连接BO、BE,
∵矩形OABC绕点B逆时针旋转得到矩形EFBG,
∴BO=BE,BA⊥OE,
∴OA=AE;
(2)∵矩形OABC绕点B逆时针旋转得到矩形EFBG,
∴AE=OA=BG=90°,
在△BGD和△EAD中,
$\left\{\begin{array}{l}{∠G=∠DAE}\\{∠BDG=∠EDA}\\{AE=GB}\end{array}\right.$,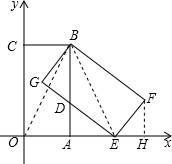
∴△BGD≌△EAD,
∴AD=GD,BD=ED,
设AD=x,则DE=BD=8-x,
∴x2+42=(8-x)2,
∴x=3,
即AD=3;
(3)如图,作FH⊥x轴于点H,
∵∠DAE=∠DEF=∠EHF=90°,
∴△DAE∽△EHF,
∴$\frac{AD}{EH}=\frac{DE}{EF}$,
∴$\frac{3}{EH}=\frac{5}{4}$,
∴EH=$\frac{12}{5}$,
∴FH=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,OH=OE+EH=$\frac{52}{5}$,
∴F($\frac{52}{5}$,$\frac{16}{5}$).
点评 本题主要考查了图形的旋转、矩形的性质、等腰三角形的性质,全等三角形的判定与性质、相似三角形的判定与性质、勾股定理的综合应用,通过作辅助线构造全等形和相似形是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:选择题
若M=(x﹣3)(x﹣5),N=(x﹣2)(x﹣6),则M与N的关系为( )
A.M=N
B.M>N
C.M<N
D.M与N的大小由x的取值而定
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=-(b-a)2 | B. | $\frac{1}{{x}^{3}}$=x-3 | C. | $\frac{{a}^{2}+1}{a+1}$=a+1 | D. | x6÷x2=x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
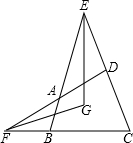 如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.
如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
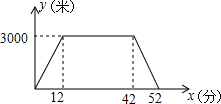 星期天,小宇同学骑自行车从家出发到图书馆查阅有关资料,之后就返回了家,如图反映了小宇离家的路程y(米)与骑车时间x(分)的函数关系.从图象得到下列信息,错误的是( )
星期天,小宇同学骑自行车从家出发到图书馆查阅有关资料,之后就返回了家,如图反映了小宇离家的路程y(米)与骑车时间x(分)的函数关系.从图象得到下列信息,错误的是( )| A. | 小宇家与图书馆之间路程是3千米 | |
| B. | 小宇在图书馆查阅资料花去了42分钟 | |
| C. | 小宇从图书馆骑车回家用了10分钟 | |
| D. | 小宇从家到图书馆骑车速度比返回的速度慢 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com