

���� ��1������ֱ������������ǻ��༴�ɽ��
��2�����ACP=�����������ACQ=60��-������CA��EQ���õ���EQC=120��+������֤�ı���EDFQ�Ǿ��Σ���֪��EQF=90�㣬����Rt��BQC�У���BQC=90��-������֪��BQF=360��-��EQC-��EQF-��BQC=60�㣬�ʡ�BQF��ֵ�������P���˶����ı��С��ʼ��Ϊһ��ֵ��
��3���߶�PA�ij�Ϊm����m��ʾ��EQ������S=$\frac{1}{2}$AP•EQ���ɵõ�S��m�ĺ�����ϵʽ��Ȼ���ö��κ���������������ֵ��
��� �⣺��1����AC��l��
���CAP=90�㣬
�֡ߡ�ACP=20�㣬
���APC=70�㣬
����ת�����ʿ�֪��BQC=��APC��
���BQC=70�㣻
��2���ߡ�ABC���������Σ�
���ACB=60�㣬
����ת�����ʿ�֪��ACP=��BCQ��
���PCQ=��ACB=60�㣬
���ACP=����
���ACQ=60��-����
��AC��l��EQ��l��
��AC��EQ��
���CEQ=180��-��60��-����=120��+����
�֡�BD��l��QE��l��QF��BD��
���ı���DEQF�Ǿ��Σ�
���EQF=90�㣬
�֡ߡ�BQC=��APC=90��-����
��BQF=360��-90��-��120��+����-��90��-����=60�㣻
���BQF��ֵ�������P���˶����ı��С��ʼ��Ϊһ��ֵ���˶�ֵΪ60�㣻
��3����AP=4��BD��l����BAD=90��-60��=30�㣬
��BD=$\frac{1}{2}$AB=2��
��QB=AP=m��BD��QF����BQF=60�㣬
��BF=$\frac{\sqrt{3}}{2}m$�����ı���DEQF�Ǿ��Σ�
��EQ=DF=2-$\frac{\sqrt{3}}{2}m$��
��S=$\frac{1}{2}$AP•EQ=$\frac{1}{2}$m��2-$\frac{\sqrt{3}}{2}$m����
��S=-$\frac{\sqrt{3}}{4}$m2+m��0��m��$\frac{4\sqrt{3}}{3}$����
��m=-$\frac{1}{2����-\frac{\sqrt{3}}{4}��}$=$\frac{2\sqrt{3}}{3}$ʱ��
��-$\frac{\sqrt{3}}{4}$��0��0��$\frac{2\sqrt{3}}{3}$��$\frac{4\sqrt{3}}{3}$��
��S�����ֵ�����ֵΪ$\frac{\sqrt{3}}{3}$��
���� ������Ҫ�����˼���֪ʶ���ۺ����úͼ��α任����ǶȵĶ�ֵ���⣬��������ʽ������ֵ�����ô�����������������⣬�������ڼ�ǿѧ����ͼ���뼸�ε��������Լ����������ۺ�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ���꼶��ѧ�ڵ�һ�ο��õ�����ѧ�Ծ��������棩 ���ͣ������
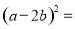 ____________________��
____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
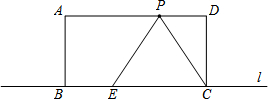 ����ABCD�ı�BC��ֱ��l�ϣ�AB=2��BC=4��P��AD����һ�����Ҳ����D�غϣ�����CP������P����APE=��CPD����ֱ��l�ڵ�E����PD�ij�Ϊx����PEC�����ABCD�غϲ��ֵ����Ϊy��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������
����ABCD�ı�BC��ֱ��l�ϣ�AB=2��BC=4��P��AD����һ�����Ҳ����D�غϣ�����CP������P����APE=��CPD����ֱ��l�ڵ�E����PD�ij�Ϊx����PEC�����ABCD�غϲ��ֵ����Ϊy��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������| A�� | 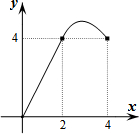 | B�� | 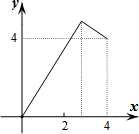 | C�� | 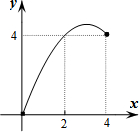 | D�� | 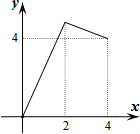 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
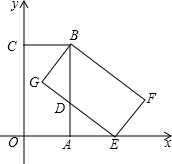 ��ͼ����֪��ֱ������ϵ�У�����OABC�ı�OA��x���������ϣ���OC��y����������ϣ�B�������Ϊ��4��8����������OABC�Ƶ�B��ʱ����ת�õ�����EFBG����Eǡ������x���ϣ�
��ͼ����֪��ֱ������ϵ�У�����OABC�ı�OA��x���������ϣ���OC��y����������ϣ�B�������Ϊ��4��8����������OABC�Ƶ�B��ʱ����ת�õ�����EFBG����Eǡ������x���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
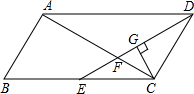 ��ͼ��?ABCD�У�AB=3cm��AD=6cm����ADC�Ľ�ƽ����DE��BC�ڵ�E����AC�ڵ�F��CG��DE������ΪG��DG=$\frac{3}{2}\sqrt{3}$cm����EF�ij�Ϊ��������
��ͼ��?ABCD�У�AB=3cm��AD=6cm����ADC�Ľ�ƽ����DE��BC�ڵ�E����AC�ڵ�F��CG��DE������ΪG��DG=$\frac{3}{2}\sqrt{3}$cm����EF�ij�Ϊ��������| A�� | 2cm | B�� | $\sqrt{3}$cm | C�� | 1cm | D�� | $\frac{2}{3}\sqrt{3}$cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
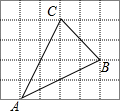 �����е�ÿ��С�����εı߳�����1����ABCÿ�����㶼������Ľ��㴦��
�����е�ÿ��С�����εı߳�����1����ABCÿ�����㶼������Ľ��㴦���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com