
分析 (1)根据题意列代数式即可;
(2)根据利润=单台利润×预订量,列出函数表达式,根据二次函数性质解决定价为多少时所获利润最大;
(3)根据题意列式计算每天最多接受的预订量,根据每天最多接受的预订量列方程求出最大量接受预订时每台售价即可.
解答 解:(1)根据题意:y=20000+$\frac{x}{100}$×10000=100x+20000;
(2)设所获的利润w(元),则W=(20000-1200-x)(100x+20000)=-100(x-400)2+36000000;
所以当降价400元,即定价为2200-400=1800元时,所获利润最大;
(2)根据题意每天最多接受50000(1-0.05)=47500台,
此时47500=100x+20000,
解得:x=275.
所以最大量接受预订时,每台定价2200-275=1925元.
点评 本题主要考查了函数实际应用问题,涉及到列代数式、求函数关系式、二次函数的性质、一元一次方程应用等知识,弄清题意,找出数量关系是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
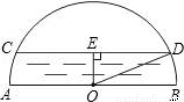
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=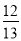 .
.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
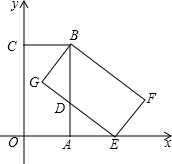 如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.
如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
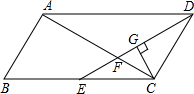 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 1cm | D. | $\frac{2}{3}\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
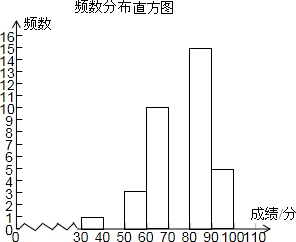 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.| 成绩分组 | 频数 | 频率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | 0.06 |
| 60≤x<70 | 10 | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com