
【题目】如图1,在平面直角坐标系中,![]() ,且满足式子
,且满足式子![]() .
.
(1)求出![]() 的值;
的值;
(2)①在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半,求出点
的面积的一半,求出点![]() 的坐标;
的坐标;
②在坐标轴的其它位置是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半仍然成立,若存在,直接写出其他符合条件的点
的面积的一半仍然成立,若存在,直接写出其他符合条件的点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 延长线上一动点,连接
延长线上一动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() ,当点
,当点![]() 运动时,求证:
运动时,求证:![]()

【答案】(1)m=-2,n=4;(2)①M的坐标为(3,0);②(-3,0)或(0,6)或(0,-6); (3)见解析
【解析】
(1)根据非负数的性质列出方程组,解方程组即可;
(2)①根据三角形的面积公式计算即可;
②分点M在x、y轴上两种情况计算;
(3)根据角平分线的定义、垂直的定义得到∠POF=∠BOF,设∠POF=∠BOF=x,∠DOE=y,结合图形得到x=y,得到答案.
解:(1)由题意得,![]() ,
,
解得m=-2,n=4;
(2)①设点M的坐标的坐标为(x,0),
△ABC的面积= ![]() ×6×2=6,
×6×2=6,
由题意得,![]() ×x×2=
×x×2=![]() ×6,
×6,
解得,x=3,
△COM的面积等于△ABC的面积的一半时,点M的坐标为(3,0);
②当点M在x轴上时,由①得,点M的坐标为(3,0)或(-3,0),
当点M在y轴上时,设点M的坐标的坐标为(0,y),
由题意得,![]() ×|y|×1=
×|y|×1=![]() ×6,
×6,
解得,y=±6,
综上所述,符合条件的点M的其他坐标为(-3,0)或(0,6)或(0,-6);
(3)∵OE平分∠AOP,
∴∠EOP=∠AOE,
∵OF⊥OE,
∴∠EOP+∠POF=90°,∠AOE+∠BOF=90°,
∴∠POF=∠BOF,
设∠POF=∠BOF=x,∠DOE=y,
∵CD⊥y轴,
∴CD∥x轴,
∴∠OPD=∠POB=2x,
则∠POD=90°-2x,
∵∠EOF=90°,
∴y+90°-2x+x=90°,
解得,x=y,
∴∠OPD=2∠DOE.


科目:初中数学 来源: 题型:
【题目】某中学开通了互联网家校合育教育平台,为了解家长使用平台的情况,学校将家长的使用情况分为”经常使用”、“偶尔使用”“和“不使用”三种类型,借助该平台大数据功能,汇总出该校八(1)班和八(2)班全体家长的使用情况,并绘制成如图所示的两幅不完整的统计图:

请根据图中信息解答下列问题
(1)此次调查的家长总人数为 ;
(2)扇形统计图中代表“不使用”类型的扇形圆心角的度数是 °,并补全条形统计图;
(3)若该校八年级学生家长共有1200人,根据此次调查结果估计该校八年级中“经常使用”类型的家长约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①c>0;
②若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ ![]() <0,
<0,
其中,正确结论的个数是( )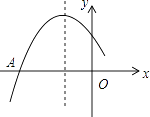
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即![]() .例如:
.例如:![]()
![]() 是
是![]() 的一种形式的配方;所以,
的一种形式的配方;所以,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出![]() 三种不同形式的配方;
三种不同形式的配方;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部明确要求中小学生每天要有2小时体育锻炼,周末朱诺和哥哥在![]() 米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
朱诺:你要![]() 分钟才能第一次追上我.
分钟才能第一次追上我.
哥哥:我骑完一圈的时候,你才骑了半圈!
(1)请根据他们的对话内容,求出朱诺和哥哥的骑行速度(速度单位:米/秒);
(2)哥哥第一次追上朱诺后,在第二次相遇前,再经过多少秒,朱诺和哥哥相距![]() 米?
米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com