练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于　　．


    8

    考点： 勾股定理；直角三角形斜边上的中线． 

    专题： 计算题．

    分析： 由“直角三角形斜边上的中线等于斜边的一半”求得AC=2DE=10；然后在直角△ACD中，利用勾股定理来求线段CD的长度即可．

    解答： 解：如图，∵△ABC中，CD⊥AB于D，E是AC的中点，DE=5，

    ∴DE=AC=5，

    ∴AC=10．

    在直角△ACD中，∠ADC=90°，AD=6，AC=10，则根据勾股定理，得

    CD===8．

    故答案是：8．

    点评： 本题考查了勾股定理，直角三角形斜边上的中线．利用直角三角形斜边上的中线等于斜边的一半求得AC的长度是解题的难点．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，等腰Rt△ABC中，∠ABC=90°，O是△ABC内一点，OA=6，OB=4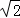，OC=10，O′为△ABC外一点，且△CBO≌△ABO′，则四边形AO′BO的面积为（　　）

    　 A． 10 B． 16 C． 40 D． 80

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    9的算术平方根是（　　）

    　 A． 3 B． ﹣3 C． 81 D． ﹣81

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    因式分解： 5x3y﹣20xy3；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


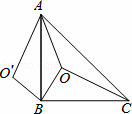
    如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB=DE，BF=CE．求证：

    （1）△ABC≌△DEF；

    （2）GF=GC．

    　

    　


    查看答案和解析>>

    科目：初中数学 来源： 题型：


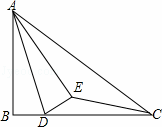
    如图，已知在Rt△ABC中，∠ABC=90°，AB=6，BC=8，点D是边BC上的任意一点，以AD为折痕翻折△ABD，使点B落在点E处，连接EC，当△DEC为直角三角形时，BD的长为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=2.5cm，PN=3cm，MN=4cm，则线段QR的长为（　　）

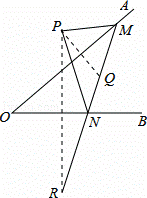
    　 A． 4.5cm B． 5.5cm C． 6.5cm D． 7cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．在一列数x1，x2，x3，…中，已知x1=1，且当k≥2时，xk=xk﹣1+1﹣4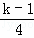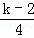（[]﹣[]）（符号[a]表示不超过实数a的最大整数，例如[2.6]=2，[0.2]=0），则x2014等于（　　）

    　 A． 1 B． 2 C． 3 D． 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    2a﹣5b+3a+b              

    查看答案和解析>>

    同步练习册答案