
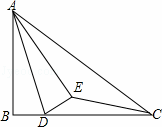
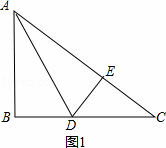
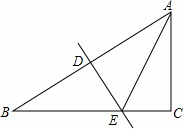
如图,已知在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是边BC上的任意一点,以AD为折痕翻折△ABD,使点B落在点E处,连接EC,当△DEC为直角三角形时,BD的长为 .
3或6
考点: 翻折变换(折叠问题).
分析: 在Rt△ABC中,∠ABC=90°,AB=6,BC=8,根据勾股定理求得AB=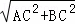 =10,根据翻折的性质得AE=AB=6,DE=BD,∠AED=∠B=90°.①如图1,当∠DEC=90°时,推出点E在线段AC上,设BD=DE=x,则CD=8﹣x,根据勾股定理即可得到结果;②如图2,当∠EDC=90,于是得到∠BDE=90°,求得∠BDA=∠ADE=45°,于是得到△ABD是等腰直角三角形于是得到结果.
=10,根据翻折的性质得AE=AB=6,DE=BD,∠AED=∠B=90°.①如图1,当∠DEC=90°时,推出点E在线段AC上,设BD=DE=x,则CD=8﹣x,根据勾股定理即可得到结果;②如图2,当∠EDC=90,于是得到∠BDE=90°,求得∠BDA=∠ADE=45°,于是得到△ABD是等腰直角三角形于是得到结果.
解答: 解:在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AB=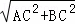 =10,
=10,
∵△AED是△ABD以AD为折痕翻折得到的,
∴AE=AB=6,DE=BD,∠AED=∠B=90°.
当△DEC为直角三角形,
①如图1,当∠DEC=90°时,
∵∠AED+∠DEC=180°,
∴点E在线段AC上,
设BD=DE=x,则CD=8﹣x,
∴CE=AB﹣AE=4,
∴DE2+CE2=CD2,
即x2+42=(8﹣x)2,
解得:x=3,
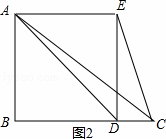
②如图2,当∠EDC=90,
∴∠BDE=90°,
∵∠BDA=∠ADE,
∴∠BDA=∠ADE=45°,
∴∠BAD=45°,
∴AB=BD=6.
综上所述:当△DEC为直角三角形时,BD的长为3或6.
故答案为:3或6.


科目:初中数学 来源: 题型:
如图,直线l:y=x+2交y轴于点A,以AO为直角边长作等腰Rt△AOB,再过B点作等腰 Rt△A1BB1交直线l于点A1,再过B1点再作等腰Rt△A2B1B2交直线l于点A2,以此类推,继续作等腰Rt△A3B2B3﹣﹣﹣,Rt△AnBn﹣1Bn,其中点A0A1A2…An都在直线l上,点B0B1B2…Bn都在x轴上,且∠A1BB1,∠A2B1B2,∠A3B2B3…∠An﹣1BnBn﹣1都为直角.则点A3的坐标为 ,点An的坐标为 .
Rt△A1BB1交直线l于点A1,再过B1点再作等腰Rt△A2B1B2交直线l于点A2,以此类推,继续作等腰Rt△A3B2B3﹣﹣﹣,Rt△AnBn﹣1Bn,其中点A0A1A2…An都在直线l上,点B0B1B2…Bn都在x轴上,且∠A1BB1,∠A2B1B2,∠A3B2B3…∠An﹣1BnBn﹣1都为直角.则点A3的坐标为 ,点An的坐标为 .
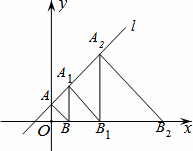
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△OAB绕点O逆时针旋转80°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是( )
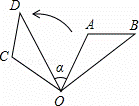
A. 30° B. 40° C. 50° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC和一点O,△ABC的顶点与点O均与小正方形的顶点重合.
(1)在方格纸中,将△ABC向下平移6个单位长度得到△A1B1C1,请画△A1B1C1.
(2)在方格纸中,将△ABC绕点O旋转180°得到△A2B2C2,请画△A2B2C2.
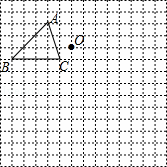
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
A. 16 B. 14 C. 12 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
马年新年即将来临,七年级(1)班课外活动小组计划做一批“中国结”.如果每人做6个,那么比计划多了7个;如果每人做5个,那么比计划少了13个.该小组计划做多少个“中国结”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com