练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     如图，长方体的底面边长分别为1cm和3cm，高为6cm，如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要多少cm？


     

    考点： 平面展开-最短路径问题． 

    分析： 要求所用细线的最短距离，需将长方体的侧面展开，进而根据“两点之间线段最短”得出结果．

    解答： 解：将长方体展开，连接A、B′，

    ∵AA′=1+3+1+3=8（cm），A′B′=6cm，

    根据两点之间线段最短，AB′==10cm．

    ∴所用细线最短需要10cm．

    点评： 本题考查了平面展开﹣最短路径问题，本题就是把长方体的侧面展开“化立体为平面”，用勾股定理解决．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    三角形两边的长是3和4，第三边的长是方程x2﹣12x+35=0的根，则该三角形的周长为（　　）

    　 A． 14 B． 12 C． 12或14 D． 以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    因式分解： 5x3y﹣20xy3；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知在Rt△ABC中，∠ABC=90°，AB=6，BC=8，点D是边BC上的任意一点，以AD为折痕翻折△ABD，使点B落在点E处，连接EC，当△DEC为直角三角形时，BD的长为　　．

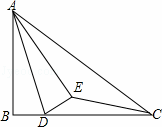
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=2.5cm，PN=3cm，MN=4cm，则线段QR的长为（　　）

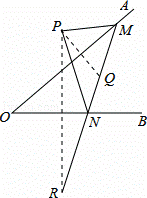
    　 A． 4.5cm B． 5.5cm C． 6.5cm D． 7cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ﹣4的相反数（　　）

    　 A． 4 B． ﹣4 C．  D． ﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．在一列数x1，x2，x3，…中，已知x1=1，且当k≥2时，xk=xk﹣1+1﹣4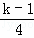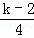（[]﹣[]）（符号[a]表示不超过实数a的最大整数，例如[2.6]=2，[0.2]=0），则x2014等于（　　）

    　 A． 1 B． 2 C． 3 D． 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察下列算式，你发现了什么规律？

    12=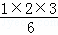；12+22=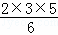；12+22+32=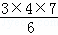；12+22+32+42=；…

    （1）根据你发现的规律，计算下面算式的值；12+22+32…+82=　204　

    （2）请用一个含n的算式表示这个规律：12+22+32…+n2=　　．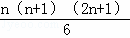

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    a，b都是示数，且a＜b，则下列不等式的变形正确的是（　　）

    　 A． a+1＞b+1 B． ﹣a＜﹣b C． 3a＜3b D．

    查看答案和解析>>

    同步练习册答案