
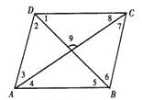
【题目】如图,若AD∥BC,AB∥DE,DF∥AC,∠OEC=72°,∠OCE=64°,则∠B=_______,∠F=_______,∠BAD=_______,∠ADF=_______.

【答案】72° 64° 108° 116°
【解析】
根据两直线平行,同位角相等可以求出∠B = 72°,∠F = 64°;根据两直线平行,同旁内角互补可以求出:∠BAD = 108°,∠ADF = 116°.
∵AB∥DE,∠OEC = 72°,
∴∠B = 72°(两直线平行,同位角相等);
∵DF∥AC,∠OCE = 64°,
∴∠F = 64°(两直线平行,同位角相等);
∵AD∥BC
∴∠B+∠BAD = 180°(两直线平行,同旁内角互补)
∴∠BAD = 180°-∠B = 180°-72° = 108°
∵AD∥BC
∴∠F+∠ADF = 180°(两直线平行,同旁内角互补)
∴∠ADF = 180°-∠F = 180°-64° = 116°
故答案为:(1)72° (2)64° (3)108° (4)116°


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】仔细阅读下面的例题:
例题:已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,则
x2-4x+m=(x+3)(x+n),
∴x2-4x+m=x2+(n+3)x+3n,
∴![]() ,解得
,解得![]() ,
,
∴另一个因式为x-7,m的值为-21.
问题:仿照以上方法解答下面的问题:
已知二次三项式2x2+3x-k有一个因式是2x-5,求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,CE平分∠ACB交AB于点E,CE=BC.
(1)求∠A的度数;
(2)能否在AC边上找一点D,并连接ED,使△AED≌△CEB?若能,请作出你找的点,并证明;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地.如图(2)是汽车行驶时离C站的路程y(千米)与行驶时间x(小时)之间的函数关系的图象.
(1)a等于多少km,AB两地的距离为多少km;
(2)求线段PM、MN所表示的y与x之间的函数表达式;
(3)求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠3和∠9是直线________、_______被直线_______所截而成的______角;∠6和∠9是直线_____、______被直线________所截而成的_______角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习:
在一次数学兴趣小组活动中,老师和几个同学一起探讨:在an=b中,a,b,n三者关系.
同学甲:已知a,n,可以求b,是我们学过的乘方运算,其中b叫做a的n次方.如:(﹣2)3=﹣8,其中﹣8是﹣2的3次方.
同学乙:已知b,n,可以求a,是我们学过的开方运算,其中a叫做b的n次方根.如:(±2)2=4,其中±2 是4的二次方根(或平方根);(﹣3)3=﹣27,其中﹣3是﹣27的三次方根(或立方根).
老师:两位同学说的很好,那么请大家计算:
(1)81的四次方根等于 ;﹣32的五次方根等于 .
同学丙:老师,如果已知a和b,那么如何求n呢?又是一种什么运算呢?
老师:这个问题问的好,已知a,b,可以求n,它是一种新的运算,称为对数运算.
这种运算的定义是:若an=b(a>0,a≠1),n叫做以a为底b的对数,记作:n=logab.例如:23=8,3叫做 以2为底8的对数,记作3=log28.根据题意,请大家计算:
(2)log327= ; (![]() )﹣2+
)﹣2+![]() ﹣log4
﹣log4![]() = .
= .
随后,老师和同学们又一起探究出对数运算的一条性质:如果a>0,a≠1,M>0,N>0,那么logaMN=logaM+logaN.
(3)请你利用上述性质计算:log53+log5![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.
(1)求证:EB=EN=EC;
(2)求证:NE2=AEDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是![]() 上的任意一点,过点C的切线分别交PA、PB于点D、E.
上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com