
如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+ kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
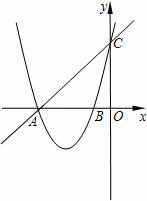
解:(1)由x=0得y=0+4=4,则点C的坐标为(0,4);
由y=0得x+4=0,解得x=﹣4,则点A的坐标为(﹣4,0);
把点C(0,4)代入y=x2+kx+k﹣1,得k﹣1=4,
解得:k=5,
∴此抛物线的解析式为y=x2+5x+4,
∴此抛物线的对称轴为x=﹣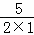 =﹣
=﹣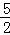 .
.
令y=0得x2+5x+4=0,
解得:x1=﹣1,x2=﹣4,
∴点B的坐标为(﹣1,0).
(2)∵A(﹣4,0),C(0,4),
∴OA=OC=4,
∴∠OCA=∠OAC.
∵∠AOC=90°,OB=1,OC=OA=4,
∴AC=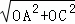 =4
=4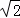 ,AB=OA﹣OB=4﹣1=3.
,AB=OA﹣OB=4﹣1=3.
∵点D在y轴负半轴上,∴∠ADC<∠AOC,即∠ADC<90°.
又∵∠ABC>∠BOC,即∠ABC>90°,∴∠ABC>∠ADC.
∴由条件“以A、C、D为顶点的三角形与△ABC相似”可得△CAD∽△ABC,
∴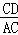 =
=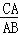 ,即
,即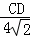 =
=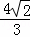 ,
,
解得:CD=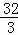 ,
,
∴OD=CD﹣CO=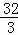 ﹣4=
﹣4=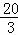 ,
,
∴点D的坐标为(0,﹣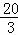 ).
).
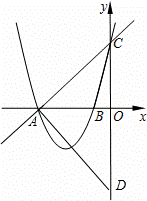


科目:初中数学 来源: 题型:
某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次 函数y=cx+
函数y=cx+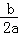 与反比例函数y=
与反比例函数y=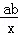 在同一坐标系内的大致图象是( )
在同一坐标系内的大致图象是( )
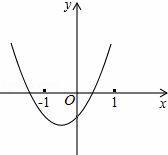
A. 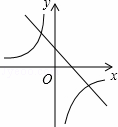 B.
B.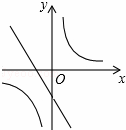 C.
C.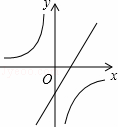 D.
D. 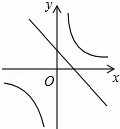
查看答案和解析>>
科目:初中数学 来源: 题型:
对于二次函数y=ax2﹣(2a﹣1)x+a﹣1(a≠0),有下列结论:
①其图象与x轴一定相交;
②若a<0,函数在x>1时,y随x的增大而减小;
③无论a取何值,抛物线的顶点始终在同一条直线上;
④无论a取何值,函数图象都经过同一个点.
其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
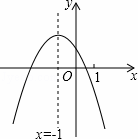
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )
A. 4个 B.3个 C 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
A. (0,2) B.(0,3) C.(0,4) D. (0,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
若点M(x,y)满足(x+y)2=x2+y2﹣2,则点M所在象限是( )
A. 第一象限或第三象限 B. 第二象限或第四象限
C. 第一象限或第二象限 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
已知点M(2a﹣5,a﹣1),分别根据下列条件求出点M的坐标.
(1)点N的坐标是(1,6),并且直线MN∥y轴;
(2)点M在第二象限,横坐标和纵坐标互为相反数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com