练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知等腰三角形的周长为24，底边y关于腰长x的函数解析式是_______．

    【答案】y=24-2x（6＜x＜12）

    【解析】

    根据周长=2x+y，可得出函数关系式，再根据三角形三边的关系确定自变量的取值范围即可．

    解：由题意得：2x+y=24，

    即可得：y=24-2x，从而可得x＜12，又∵两边之和大于第三边，

    ∴x＞6，

    可得函数关系式为：y=24-2x，自变量的取值范围为：6＜x＜12

    故答案为：y=24-2x（6＜x＜12）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )

    A. 32cm B. 24cm C. 18cm D. 16cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了搞活经济，某商场将一种商品A按标价9折出售，仍获利润10%，若商品A标价为33元，那么商品进货价为（　　）

    A. 31元 B. 30.2元 C. 29.7元 D. 27元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a <－1，则方程x2＋(1－2a)x＋a2＝0根的情况是

    A. 有两个不相等的实数根 B. 有两个相等的实根

    C. 没有实数根 D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列条件中，能判定两个直角三角形全等的个数有_____个．①两条直角边对应相等；②斜边和一锐角对应相等；③斜边和一条直角边对应相等；④面积相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在矩形 ABCD中，AB＝10cm，BC＝8cm．点P从A出发，沿A→B→C→D路线运动，到D停止；点Q从D出发，沿 D→C→B→A路线运动，到A停止．若点P、点Q同时出发，点P的速度为每秒1cm，点Q的速度为每秒2cm，a秒时点P、点Q同时改变速度，点P的速度变为每秒bcm，点Q的速度变为每秒dcm．图②是点P出发x秒后△APD的面积S1（cm2）与x（秒）的函数关系图象；图③是点Q出发x秒后△AQD的面积S2（cm2）与x（秒）的函数关系图象．

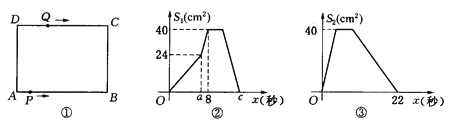
    （1）、参照图象，求b、图②中c及d的值；

    （2）、连接PQ，当PQ平分矩形ABCD的面积时，运动时间x的值为 ；

    （3）、当两点改变速度后，设点P、Q在运动线路上相距的路程为y（cm），求y（cm）与运动时间x（秒）之间的函数关系式，并写出自变量x的取值范围；

    （4）、若点P、点Q在运动路线上相距的路程为25cm，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下问题，不适合用全面调查的是（ ）

    A. 旅客上飞机前的安检 B. 学校招聘教师，对应聘人员的面试

    C. 了解全校学生的课外读书时间 D. 了解全国中学生的用眼卫生情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在郴州市中小学“创园林城市，创卫生城市，创文明城市”演讲比赛中，5位评委给靓靓同学的评分如下：9.0，9.2，9.2，9.1，9.5，则这5个数据的平均数和众数分别是（　　）

    A. 9.1，9.2 B. 9.2，9.2 C. 9.2，9.3 D. 9.3，9.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店准备购进甲、乙两种商品．已知甲商品每件进价15元，售价20元；乙商品每件进价35元，售价45元．

    （1）若该商店同时购进甲、乙两种商品共100件，恰好用去3100元，求购进甲、乙两种商品各多少件？

    （2）若该商店准备购进甲、乙两种商品共100件，其中甲种商品应多于30件且这两种商品全部售出后获利不少于840元，问应该怎样进货，才能使总利润最大，最大利润是多少？（利润=售价﹣进价）

    查看答案和解析>>

    同步练习册答案