
【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F. 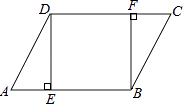
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.
【答案】
(1)证明:∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°,
∵四边形ABCD为平行四边形,
∴AD=BC,∠A=∠C,
在△ADE和△CBF中,
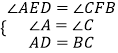 ,
,
∴△ADE≌△CBF(AAS)
(2)证明:∵四边形ABCD为平行四边形,
∴CD∥AB,
∴∠CDE+∠DEB=180°,
∵∠DEB=90°,
∴∠CDE=90°,
∴∠CDE=∠DEB=∠BFD=90°,
则四边形BFDE为矩形
【解析】(1)由DE与AB垂直,BF与CD垂直,得到一对直角相等,再由ABCD为平行四边形得到AD=BC,对角相等,利用AAS即可的值;(2)由平行四边形的对边平行得到DC与AB平行,得到∠CDE为直角,利用三个角为直角的四边形为矩形即可的值.
【考点精析】本题主要考查了平行四边形的性质和矩形的判定方法的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知今年小明的年龄是![]() 岁,小红的年龄比小明的2倍少4岁,小华的年龄比小红的
岁,小红的年龄比小明的2倍少4岁,小华的年龄比小红的![]() 还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含
还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含![]() 的式子表示小刚的年龄,并计算当
的式子表示小刚的年龄,并计算当![]() 时小刚的年龄.
时小刚的年龄.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂今年3月的产值为50万元,5月份上升到72万元,这两个月平均每月增长的百分率是多少?若设平均每月增长的百分率为x,则列出的方程正确的是( )
A.50(1+x)=72B.50(1+x)+50(1+x)2=72
C.50(1+x)×2=72D.50(1+x)2=72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点. 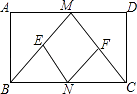
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=时,四边形MENF是正方形(只写结论,不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为( )
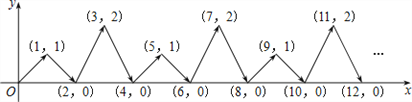
A. (2017,1) B. (2017,0) C. (2017,2) D. (2016,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com