
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点. 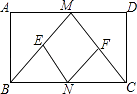
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=时,四边形MENF是正方形(只写结论,不需证明).
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D=90°,
又∵M是AD的中点,
∴AM=DM.
在△ABM和△DCM中,
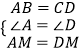 ,
,
∴△ABM≌△DCM(SAS)
(2)解:四边形MENF是菱形.
证明如下:
∵E,F,N分别是BM,CM,CB的中点,
∴NE∥MF,NE=MF.
∴四边形MENF是平行四边形.
由(1),得BM=CM,∴ME=MF.
∴四边形MENF是菱形
(3)2:1
【解析】(3)解: 当AD:AB=2:1时,四边形MENF是正方形.理由:
∵M为AD中点,
∴AD=2AM.
∵AD:AB=2:1,
∴AM=AB.
∵∠A=90,
∴∠ABM=∠AMB=45°.
同理∠DMC=45°,
∴∠EMF=180°﹣45°﹣45°=90°.
∵四边形MENF是菱形,
∴菱形MENF是正方形.
故答案为:2:1.
(1)根据矩形的性质可得AB=CD,∠A=∠D=90°,再根据M是AD的中点,可得AM=DM,然后再利用SAS证明△ABM≌△DCM;(2)四边形MENF是菱形.首先根据中位线的性质可证明NE∥MF,NE=MF,可得四边形MENF是平行四边形,再根据△ABM≌△DCM可得BM=CM进而得ME=MF,从而得到四边形MENF是菱形;(3)当AD:AB=2:1时,四边形MENF是正方形,证明∠EMF=90°根据有一个角为直角的菱形是正方形得到结论.


科目:初中数学 来源: 题型:
【题目】下列事件中,随机事件是( )
A.任意画一个三角形,其内角和为180°B.经过有交通信号的路口,遇到红灯
C.在只装了红球的袋子中摸到白球D.太阳从东方升起
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
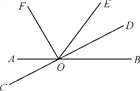
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标为( )
A. (3,3) B. (6,-6) C. (3,3)或(6,-6) D. (3,-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com