
 如图,在直角坐标系中,⊙P的圆心坐标为(0,-1),A(1,-2)是⊙P上一点,与⊙P相切于点A的直线与坐标轴交于点B,C.求线段BC的长.
如图,在直角坐标系中,⊙P的圆心坐标为(0,-1),A(1,-2)是⊙P上一点,与⊙P相切于点A的直线与坐标轴交于点B,C.求线段BC的长. 分析 连接PA,AH⊥y轴于H,如图,有点A点和P点坐标得到AH=1,OH=2,OP=1,则PH=1,于是可判断△APH为等腰直角三角形,接着利用切线的性质可判断PA⊥BC,所以△APB为等腰直角三角形,则PH=BH=1,于是BC=$\sqrt{2}$OB=3$\sqrt{2}$.
解答 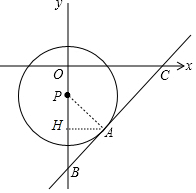 解:连接PA,AH⊥y轴于H,如图,
解:连接PA,AH⊥y轴于H,如图,
∵A(1,-2),P(0,-1),
∴AH=1,OH=2,OP=1,
∴PH=1,
∴△APH为等腰直角三角形,
∴∠APH=45°,
∵BC为切线,
∴PA⊥BC,
∴∠PAB=90°,
∴△APB为等腰直角三角形,
∴PH=BH=1,∠PBA=45°,
∴△OBC为等腰直角三角形,
∴BC=$\sqrt{2}$OB=3$\sqrt{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.也考查了等腰直角三角的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | x2+$\frac{2}{5}$x+2=0 | B. | x2-$\frac{2}{5}$x-2=0 | C. | x2+$\frac{2}{5}$x+10=0 | D. | x2-2x-10=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
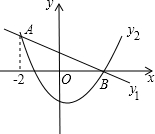 直线y1=kx+m与抛物线y2=ax2+bx+c在同一坐标中的图象如图所示,直线与抛物线相交于A(-2,2)、B(3,0),当x取值范围是-2<x<3时,y1>y2.
直线y1=kx+m与抛物线y2=ax2+bx+c在同一坐标中的图象如图所示,直线与抛物线相交于A(-2,2)、B(3,0),当x取值范围是-2<x<3时,y1>y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是长方形鸡场平面示意图,一边靠墙,并且墙长为18米,另外三面用竹篱笆围成,若竹篱笆总长为35m.
如图,是长方形鸡场平面示意图,一边靠墙,并且墙长为18米,另外三面用竹篱笆围成,若竹篱笆总长为35m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com