
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌХзЮяЯпy=-![]() x2+bx+cНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуC,жБЯпy=x+6ОЙ§AЁЂCСНЕуЃЎ
x2+bx+cНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуC,жБЯпy=x+6ОЙ§AЁЂCСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧЕкЖўЯѓЯоХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPQЁЮAC,PQНЛжБЯпBCгкЕуQЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЕуQЕФКсзјБъЮЊm,ЧѓmгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌзїЕуPЙигкжБЯпACЕФЖдГЦЕуЕуK,СЌНгQK,ЕБЕуKТфдкжБЯпy=-![]() xЩЯЪБЃЌЧѓЯпЖЮQKЕФГЄ.
xЩЯЪБЃЌЧѓЯпЖЮQKЕФГЄ.



ЁОД№АИЁП(1) y=-![]() x2-x+6ЃЛЃЈ2ЃЉm=
x2-x+6ЃЛЃЈ2ЃЉm=![]() t2+
t2+![]() tЃЛЃЈ3ЃЉ
tЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮі:(1)ЯШИљОнвЛДЮКЏЪ§ЧѓГіA,CЕузјБъ,ШЛКѓАбA,CДњШыЖўДЮКЏЪ§НтЮіЪННтЗНГЬзщМДПЩЧѓГіЖўДЮКЏЪ§НтЮіЪН,(2)ИљОнPQЁЮAC,ЧѓПЩЕУPQЫљдкжБЯпНтЮіЪНжаЕФk,ИљОнPЕузјБъПЩБэЪОPQЕФжБЯпНтЮіЪН,ШЛКѓдйСЊСЂPQКЭBCМДПЩЧѓНт,(3)ЯШИљОнЕуPЙигкжБЯпACЕФЖдГЦЕуK,ИљОнжаЕузјБъЙЋЪНБэЪОГіЕуK,ШЛКѓДњШыжБЯпy=Ѓ![]() x,ПЩЧѓГіЕуK,ШЛКѓИљОнСНЕуМфОрРыЙЋЪНПЩЧѓНтQK.
x,ПЩЧѓГіЕуK,ШЛКѓИљОнСНЕуМфОрРыЙЋЪНПЩЧѓНтQK.
ЪдЬтНтЮі:(1) вђЮЊжБЯпy=x+6ОЙ§A,CСНЕу,
ЫљвдA(Ѓ6,0),C(0,6),
вђЮЊХзЮяЯпy=![]() x2+bx+cОЙ§A,CСНЕу,АбA(Ѓ6,0),C(0,6)ДњШыПЩЕУ:
x2+bx+cОЙ§A,CСНЕу,АбA(Ѓ6,0),C(0,6)ДњШыПЩЕУ:
 ,
,
НтЕУ: ![]() ,
,
ЫљвдЖўДЮКЏЪ§НтЮіЪНЮЊ: ![]() ,
,
(2)вђЮЊPЕудкХзЮяЯпЩЯ,ЫљвдPЕузјБъЪЧ(t, ![]() ),QЕудкжБЯпBCЩЯ,
),QЕудкжБЯпBCЩЯ,
ЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+b,ИљОнЬтвтПЩЕУ:
![]() ,НтЕУ:
,НтЕУ: ![]() ,
,
ЫљвджБЯпBCЕФНтЮіЪНЮЊ: y=Ѓ2x+6,
вђЮЊPQЁЮAC,
ЫљвдПЩЕУЮЊ: ![]() НтЕУ:
НтЕУ: ![]() ,
,
ЫљвджБЯпPQЕФжБЯпНтЮіЪНЮЊ: y=x+![]() ,
,
НЋжБЯпPQКЭжБЯпBCСЊСЂПЩЧѓЕУQЕФКсзјБъ:
Ѓ2x+6= x+![]() ,
,
Ѓ3x=![]() ,
,
x= ![]() ,
,
Ыљвдm= ![]() ,
,
(3)ИљОнЬтвтПЩЕУ:жБЯпQKгкжБЯпACДЙжБ,ПЩЕУ:
![]() ,НтЕУ:
,НтЕУ: ![]()
ЫљвджБЯпQKЕФНтЮіЪНЮЊ: y=Ѓx+![]() ,
,
СЊСЂжБЯпQKКЭжБЯпAC,ПЩЧѓЕУСНжБЯпЕФНЛЕуКсзјБъ:
Ѓx+![]() = x+6,
= x+6,
НтЕУ: x=![]() ,
,
ЫљвдНЛЕузнзјБъЮЊ: y=![]() ,
,
ИљОнжаЕузјБъЙЋЪНПЩЕУKЕФзјБъЮЊ(![]() ,
,![]() ),
),
вђЮЊKдкy=Ѓ![]() xЩЯ,
xЩЯ,
Ыљвд![]() ,НтЕУ:
,НтЕУ:
вђЮЊQЕФзјБъЮЊ(![]() ,
,![]() ), KЕФзјБъЮЊ(
), KЕФзјБъЮЊ(![]() ,
,![]() ),
),
ИљОнСНЕужЎМфОрРыЙЋЪНПЩЕУ:
QK=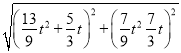 =
=![]() .
.
ЕуОІ:БОЬтжївЊПМВщЖўДЮКЏЪ§ЭМЯѓаджЪ,вЛДЮКЏЪ§ЭМЯёаджЪ,НтОіБОЬтЕФЙиМќЪЧФмЙЛгУД§ЖЈЯЕЪ§ЗЈЧѓГівЛДЮКЏЪ§НтЮіЪН,ВЂСЊСЂЖўДЮКЏЪ§НтЮіЪНЧѓКЏЪ§ЕФНЛЕуЪЧНтОіБОЬтЕФЙиМќ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫжБЙлЕиБэЪОФГЕиФГШе24аЁЪБЕФЦјЮТЫцЪБПЬБфЛЏЕФЧїЪЦЃЌзюЪЪКЯЪЙгУЕФЭГМЦЭМЪЧЃЈ ЃЉ
A.ЩШаЮЭМB.ЬѕаЮЭМC.елЯпЭМD.вдЩЯД№АИЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЭЌбЇШЅФГХњСуМцгЊЕФЮФОпЕъЃЌЮЊбЇаЃУРЪѕаЁзщЕФ30УћЭЌбЇЙКТђЧІБЪКЭЯ№ЦЄ.ШєИјШЋзщУПШЫИїТђ2жЇЧІБЪКЭ1ПщЯ№ЦЄЃЌФЧУДашАДСуЪлМлЙКТђЃЌЙВжЇИЖ30дЊЃЛШєИјШЋзщУПШЫИїТђ3жЇЧІБЪКЭ2ПщЯ№ЦЄЃЌФЧУДПЩАДХњЗЂМлЙКТђЃЌЙВжЇИЖ40.5дЊ.вбжЊ1жЇЧІБЪЕФХњЗЂМлБШСуЪлМлЕЭ0.05дЊЃЌ1ПщЯ№ЦЄЕФХњЗЂМлБШСуЪлМлЕЭ0.10дЊ.ЧыНтОіЯТСаЮЪЬтЃЈОљашаДГіНтЬтЙ§ГЬЃЉЃК
ЃЈ1ЃЉЮЪетМвЮФОпЕъУПжЇЧІБЪКЭУППщЯ№ЦЄЕФХњЗЂМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉаЁССЭЌбЇгУ4дЊЧЎдкетМвЮФОпЕъАДСуЪлМлТђЭЌбљЕФЧІБЪКЭЯ№ЦЄЃЈСНбљЖМвЊТђЃЌ4дЊЧЎЧЁКУгУЭъЃЉЃЌгаФФМИжжЙКТђЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗжНтвђЪНЃК
ЃЈ1ЃЉ4a3ЉaЃЛ
ЃЈ2ЃЉ9+6ЃЈa+bЃЉ+ЃЈa+bЃЉ2ЃЛ
ЃЈ3ЃЉЉ8ax2+16axyЉ8ay2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЎЫЕУї
ЃЎЫЕУї![]() ЕФРэгЩЃЎ
ЕФРэгЩЃЎ

НтЃКвђЮЊ![]() ЃЈвбжЊЃЉЃЌ
ЃЈвбжЊЃЉЃЌ
Ыљвд![]() ЁЮ
ЁЮ![]() ЃЈ________________________________ЃЉЃЎ
ЃЈ________________________________ЃЉЃЎ
Ыљвд![]() ЃЈ_____________________________ЃЉЃЎ
ЃЈ_____________________________ЃЉЃЎ
вђЮЊ![]() ЦНЗж
ЦНЗж![]() ЃЈвбжЊЃЉЃЌ
ЃЈвбжЊЃЉЃЌ
Ыљвд![]() ЃЈ_______________________________ЃЉ.
ЃЈ_______________________________ЃЉ.
ЭЌРэ![]() .
.
Ыљвд![]() ЃЈ___________________________________ЃЉЃЎ
ЃЈ___________________________________ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдк![]() жаЃЌ
жаЃЌ ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌ
ЃЌ ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌ
ЃЌ ![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЃЌСЌНс
БпЕФжаЕуЃЌСЌНс![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ

ЃЈ![]() ЃЉВТЯы
ЃЉВТЯы![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ![]() ЃЉШє
ЃЉШє![]() ЃЌ
ЃЌ ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌЁЯBЃН30ЁуЃЌвдAЮЊдВаФЃЌШЮвтГЄЮЊАыОЖЛЛЁЗжБ№НЛABЁЂACгкЕуMКЭNЃЌдйЗжБ№вдMЁЂNЮЊдВаФЃЌДѓгк![]() MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНгAPЃЌВЂбгГЄНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНгAPЃЌВЂбгГЄНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ

ЂйADЪЧЁЯBACЕФЦНЗжЯпЃЛЂкЁЯADCЃН60ЁуЃЛЂлЕуDдкABЕФДЙжБЦНЗжЯпЩЯЃЛЂмШєAC=![]() dmЃЌAD=2dmЃЌдђЕуDЕНABЕФОрРыЪЧ1dmЃЛЂнSЁїDACЁУSЁїDABЃНACЁУABЃН1ЁУ2
dmЃЌAD=2dmЃЌдђЕуDЕНABЕФОрРыЪЧ1dmЃЛЂнSЁїDACЁУSЁїDABЃНACЁУABЃН1ЁУ2
A. 2 B. 3 C. 4 D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМКжЊ:ШчЭМЂйЃЌжБЯп![]() жБЯп
жБЯп![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌЕу
ЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯ(
ЩЯ(![]() ЁЂ
ЁЂ![]() ВЛгы
ВЛгы![]() ЕужиКЯ)ЃЌЕу
ЕужиКЯ)ЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЧв
ЩЯЧв![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() .Еу
.Еу![]() дкЕу
дкЕу![]() ЕФзѓБпЧв
ЕФзѓБпЧв![]()

(1)жБНгаДГіЕФ![]() УцЛ§ ;
УцЛ§ ;
(2)ШчЭМЂкЃЌШє![]() ЃЌзї
ЃЌзї![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гк
гк![]() ЃЌНЛ
ЃЌНЛ![]() гк
гк![]() ЃЌЪдЫЕУї
ЃЌЪдЫЕУї![]() ;
;


(3)ШчЭМЂлЃЌШє![]() ЃЌЕу
ЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯдЫЖЏЃЌ
ЩЯдЫЖЏЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ,дкЕу
,дкЕу![]() дЫЖЏЙ§ГЬжа
дЫЖЏЙ§ГЬжа![]() ЕФжЕЪЧЗёБфЛЏ?ШєВЛБфЃЌЧѓГіЦфжЕ;ШєБфЛЏЃЌЧѓГіБфЛЏЗЖЮЇ.
ЕФжЕЪЧЗёБфЛЏ?ШєВЛБфЃЌЧѓГіЦфжЕ;ШєБфЛЏЃЌЧѓГіБфЛЏЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЃЌ
ЃЌ ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ ![]() Йигк
Йигк![]() ЕФЖдГЦЭМаЮЮЊ
ЕФЖдГЦЭМаЮЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЂйЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкШєЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЖЏЕуЃЈВЛгыЕу
ЩЯвЛЖЏЕуЃЈВЛгыЕу![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌвЛЖЏЕу
ЃЌвЛЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд![]() ЕФЫйЖШбиЯпЖЮ
ЕФЫйЖШбиЯпЖЮ![]() дШЫйдЫЖЏЕНЕу
дШЫйдЫЖЏЕНЕу![]() ЃЌдйвд
ЃЌдйвд![]() ЕФЫйЖШбиЯпЖЮ
ЕФЫйЖШбиЯпЖЮ![]() дШЫйдЫЖЏЕНЕу
дШЫйдЫЖЏЕНЕу![]() ЃЌЕНДяЕу
ЃЌЕНДяЕу![]() КѓЭЃжЙдЫЖЏЃЎЕБЕу
КѓЭЃжЙдЫЖЏЃЎЕБЕу![]() биЩЯЪіТЗЯпдЫЖЏЕНЕу
биЩЯЪіТЗЯпдЫЖЏЕНЕу![]() ЫљашвЊЕФЪБМфзюЖЬЪБЃЌЧѓ
ЫљашвЊЕФЪБМфзюЖЬЪБЃЌЧѓ![]() ЕФГЄКЭЕу
ЕФГЄКЭЕу![]() зпЭъШЋГЬЫљашЕФЪБМфЃЎ
зпЭъШЋГЬЫљашЕФЪБМфЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com