
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
(1)求证:AB是⊙O的切线;
(2)若∠A=60°,DF= ![]() ,求⊙O的直径BC的长.
,求⊙O的直径BC的长.
【答案】
(1)
证明:∵CD=CB,
∴∠CBD=∠CDB,
∵AB是⊙O的直径,
∴∠CBE=90°,
∴∠CBD+∠BCE=∠CDB+∠DCE,
∴∠BCE=∠DCE,
即∠BCD=2∠BCE,
∵∠BCD=2∠ABD,
∴∠ABD=∠BCE,
∴∠CBD+∠ABD=∠CBD+∠BCE=90°,
∴CB⊥AB,
∵CB为直径,
∴AB是⊙O的切线
(2)
解:∵∠A=60°,DF= ![]() ,
,
∴在Rt△AFD中,AF= ![]() =
= ![]() =1,
=1,
在Rt△BFD中,BF=DFtan60°= ![]() ×
× ![]() =3,
=3,
∵DF⊥AB,CB⊥AB,
∴DF∥BC,
∴∠ADF=∠ACB,
∵∠A=∠A,
∴△ADF∽△ACB,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CB=4 ![]() .
.
【解析】此题考查了切线的判定、等腰三角形的性质以及相似三角形的判定与性质.注意证得△ADF∽△ACB是解此题的关键.
(1)由CD=CB,∠BCD=2∠ABD,可证得∠BCE=∠ABD,继而求得∠ABC=90°,则可证得AB是⊙O的切线;(2)由∠A=60°,DF= ![]() ,可求得AF、BF的长,易证得△ADF∽△ACB,然后由相似三角形的对应边成比例,求得答案.
,可求得AF、BF的长,易证得△ADF∽△ACB,然后由相似三角形的对应边成比例,求得答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将连续的奇数 1,3,5,7,9,…,排成如图的数阵.
(1)十字框中的五个数的和与中间数 15 有什么关系?
(2)设中间数为 a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于 2 005 吗?若能,请写出这五个数;若不能, 说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④△PBF是等边三角形,其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④△PBF是等边三角形,其中正确的是( )

A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】OC把∠AOB分成两部分且有下列两个等式成立:
①∠AOC=![]() 直角+
直角+![]() ∠BOC;②∠BOC=
∠BOC;②∠BOC=![]() 平角-
平角-![]() ∠AOC,问∶
∠AOC,问∶
(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
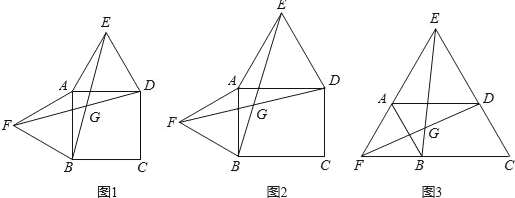
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com