Question

【题目】如图，双曲线y=（x＞0）经过△OAB的顶点A和OB的中点C．AB∥x轴，点A的坐标为（4，6），连接AC交x轴于D．连接BD．

（1）确定k的值；

（2）求直线AC的解析式；

（3）判断四边形OABD的形状，并说明理由；

（4）求△OAC的面积．

Answer 1

【答案】（1）-（2）直线AC解析式为y=-x+9；（3）四边形OABC为平行四边形，理由见解析；（4）18.

【解析】

试题分析：（1）把A的坐标代入反比例解析式求出k的值即可；

（2）由AB与x轴平行，且A纵坐标为6，得到B纵坐标为6，再由C为OB中点，确定出C纵坐标为3，代入反比例解析式确定出C坐标，利用待定系数法确定出直线AC解析式即可；

（3）四边形OABC为平行四边形，理由为：由C的坐标确定出B的坐标，进而确定出AB的长，由直线AC与x轴的交点为D，确定出D坐标，得出OD的长，由AB与OD平行且相等，得到四边形OABC为平行四边形；

（4）由四边形OABC为平行四边形，得到对角线互相平分，得到三角形AOC面积为平行四边形面积的四分之一，求出即可．

试题解析：（1）将A（4，6）代入解析式y=得：k=24；

（2）∵AB∥x轴，B的纵坐标是6，C为OB中点，

∴把y=3代入反比例解析式得：x=8，即C坐标为（8，3），

设直线AC的解析式为y=kx+b，

将A（4，6）与C（8，3）代入得：

，

解得：，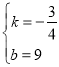

则直线AC解析式为y=-x+9；

（3）四边形OABC为平行四边形，理由为：

∵点C的坐标为（8，3），

∴B的坐标为（16，6），即AB=12，

把y=0代入y=-x+9中得：x=12，即D（12，0），

∴OD=12，

∴AB=OD，

∵AB∥OD，

∴四边形OABC为平行四边形；

（4）∵S四边形OABC=12×6=72，

∴S△OAC=S四边形OABC=18．