
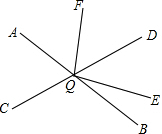
 如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.
如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.| 1 |
| 2 |
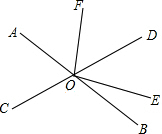 解:∵OF平分∠AOD,
解:∵OF平分∠AOD,| 1 |
| 2 |


科目:初中数学 来源: 题型:
 下图描述了小丽散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.依据图象,下面描述符合小红散步情景的是( )
下图描述了小丽散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.依据图象,下面描述符合小红散步情景的是( )| A、从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 |
| B、从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了 |
| C、从家出发,一直散步(没有停留),然后回家了 |
| D、从家出发,散了一会儿步,就找同学去了,18分钟后才开始返回 |
查看答案和解析>>
科目:初中数学 来源: 题型:
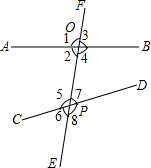 如图,直线AB,CD与直线EF分别交于点O,P.
如图,直线AB,CD与直线EF分别交于点O,P.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
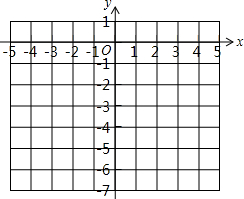 函数y=ax2与直线y=-2x-4交于点(2,b).
函数y=ax2与直线y=-2x-4交于点(2,b).| … | … | ||||||||
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com