
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 .


7【考点】全等三角形的判定与性质;线段垂直平分线的性质;勾股定理;矩形的性质.
【专题】几何图形问题.
【分析】根据线段中点的定义可得CG=DG,然后利用“角边角”证明△DEG和△CFG全等,根据全等三角形对应边相等可得DE=CF,EG=FG,设DE=x,表示出BF,再利用勾股定理列式求EG,然后表示出EF,再根据线段垂直平分线上的点到两端点的距离相等可得BF=EF,然后列出方程求出x的值,从而求出AD,再根据矩形的对边相等可得BC=AD.
【解答】解:∵矩形ABCD中,G是CD的中点,AB=8,
∴CG=DG=
 ×8=4,
×8=4,
在△DEG和△CFG中,

 ,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
设DE=x,
则BF=BC+CF=AD+CF=4+x+x=4+2x,
在Rt△DEG中,EG=
 =
=
 ,
,
∴EF=2
 ,
,
∵FH垂直平分BE,
∴BF=EF,
∴4+2x=2
 ,
,
解得x=3,
∴AD=AE+DE=4+3=7,
∴BC=AD=7.
故答案为:7.
【点评】本题考查了全等三角形的判定与性质,矩形的性质,线段垂直平分线上的点到两端点的距离相等的性质,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.


科目:初中数学 来源: 题型:
.在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若DE=
 BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.


查看答案和解析>>
科目:初中数学 来源: 题型:
电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(2014•扬州)如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )


A.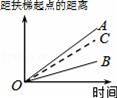
 B.
B.

C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
在劳技课上,老师请同学们在一张长为9cm,宽为8cm的长方形纸板上,剪下一个腰长为5cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边长上).请你帮助同学们画出图形并计算出剪下的等腰三角形的面积.(求出所有可能的情况)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com